题目内容
已知等差数列{an}中,公差d>0,其前n项和为Sn,且满足a2•a3=45,a1=a4=14.
(1)求数列{an}的通项公式;
(2)设由bn=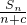 (c≠0)构成的新数列为{bn},求证:当且仅当c=-
(c≠0)构成的新数列为{bn},求证:当且仅当c=- 时,数列{bn}是等差数列;
时,数列{bn}是等差数列;
(3)对于(2)中的等差数列{bn},设cn=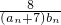 (n∈N*),数列{cn}的前n项和为Tn,现有数列{f(n)},f(n)=Tn•(an+3-
(n∈N*),数列{cn}的前n项和为Tn,现有数列{f(n)},f(n)=Tn•(an+3-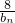 )•0.9n(n∈N*),是否存在n0∈N*,使f(n)≤f(n0)对一切n∈N*都成立?若存在,求出n0的值,若不存在,请说明理由.
)•0.9n(n∈N*),是否存在n0∈N*,使f(n)≤f(n0)对一切n∈N*都成立?若存在,求出n0的值,若不存在,请说明理由.
解:(1)∵等差数列{an}中,公差d>0,
∴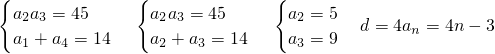 (3分)
(3分)
(3分)
(2)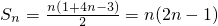 ,
,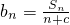 =
=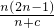 ,
,
由2b2=b1+b3得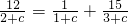 ,化简得2c2+c=0,c≠0,
,化简得2c2+c=0,c≠0,
∴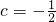
反之,令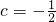 ,即得bn=2n,显然数列{bn}为等差数列,
,即得bn=2n,显然数列{bn}为等差数列,
∴当且仅当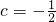 时,数列{bn}为等差数列.(9分)
时,数列{bn}为等差数列.(9分)
(3)cn=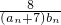 =
=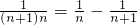 ,∴
,∴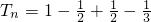 +
+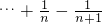
f(n)=Tn•(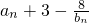 )•0.9n=
)•0.9n=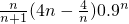 =4(n-1)•0.9n(11分)
=4(n-1)•0.9n(11分)
∵f(n+1)-f(n)=4•0.9n[0.9n-(n-1)]=4•0.9n[1-0.1n]n∈N+
∴当n<10时,f(n+1)>f(n),当n=10时,f(n+1)=f(n),当n>10时,f(n+1)<f(n),
f(n)max=f(10)=f(11),(13分)
∴存在n0=10或11,使f(n)≤f(n0)对一切n∈N*都成立.(14分)
分析:(1)根据题意,由等差数列的性质,有a1+a4=a2+a3=14,与a2•a3=45联立,计算可得数列{an}的通项公式;
(2)首先计算Sn,代入数列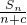 ,可得其通项公式,运用等差中项的性质分析,可得答案.
,可得其通项公式,运用等差中项的性质分析,可得答案.
(3)求出cn的表达式,数列{cn}的前n项和为Tn,得到f(n)的关系式,通过作差法对n讨论,求出n的取值,
点评:本题考查等差数列的通项公式的运用,注意结合等差数列的性质分析,可以减少运算量,降低难度.考查数列的求和,解题的方法是解方程与不等式的思想,体现的数学思想是转化思想.
∴
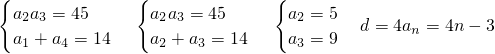 (3分)
(3分)(3分)
(2)
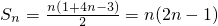 ,
,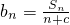 =
=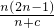 ,
,由2b2=b1+b3得
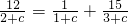 ,化简得2c2+c=0,c≠0,
,化简得2c2+c=0,c≠0,∴
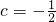
反之,令
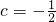 ,即得bn=2n,显然数列{bn}为等差数列,
,即得bn=2n,显然数列{bn}为等差数列,∴当且仅当
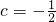 时,数列{bn}为等差数列.(9分)
时,数列{bn}为等差数列.(9分)(3)cn=
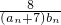 =
=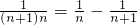 ,∴
,∴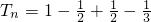 +
+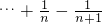
f(n)=Tn•(
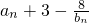 )•0.9n=
)•0.9n=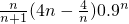 =4(n-1)•0.9n(11分)
=4(n-1)•0.9n(11分)∵f(n+1)-f(n)=4•0.9n[0.9n-(n-1)]=4•0.9n[1-0.1n]n∈N+
∴当n<10时,f(n+1)>f(n),当n=10时,f(n+1)=f(n),当n>10时,f(n+1)<f(n),
f(n)max=f(10)=f(11),(13分)
∴存在n0=10或11,使f(n)≤f(n0)对一切n∈N*都成立.(14分)
分析:(1)根据题意,由等差数列的性质,有a1+a4=a2+a3=14,与a2•a3=45联立,计算可得数列{an}的通项公式;
(2)首先计算Sn,代入数列
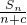 ,可得其通项公式,运用等差中项的性质分析,可得答案.
,可得其通项公式,运用等差中项的性质分析,可得答案.(3)求出cn的表达式,数列{cn}的前n项和为Tn,得到f(n)的关系式,通过作差法对n讨论,求出n的取值,
点评:本题考查等差数列的通项公式的运用,注意结合等差数列的性质分析,可以减少运算量,降低难度.考查数列的求和,解题的方法是解方程与不等式的思想,体现的数学思想是转化思想.

练习册系列答案
相关题目
 已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.
已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.