Question

设A（-1，2），B（3，1），若直线y=kx与线段AB没有公共点，则k的取值范围是（　　）

• A．（-ω，-2）∪（

  1

  3

  ，+ω）
• B．（-ω，-

  1

  3

  ）∪（2，+ω）
• C．（-

  1

  3

  ，2）
• D．（-2，

  1

  3

  ）

Answer 1

分析：直线y=kx过定点（0，0），再求它与两点A（-1，2），B（3，1）的斜率，即可取得k的取值范围．

解答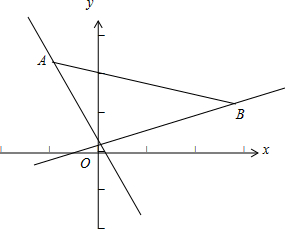：解：直线y=kx过定点（0，0），则K_AO=

2-0

-1-0

=-2，K_OB=

1-0

3-0

=

1

3

，
由图象可知：当直线在OB与x的正向之间或在OA与x的负向之间符合题意，
所以k的取值范围是：（-2，0）∪[0，

1

3

）=（-2，

1

3

）
故选D

点评：本题为斜率范围的求解，求对边界的斜率是解决问题的关键，属基础题．