题目内容
点M在圆（x-5）2+（y-3）2=9上，则M点到直线3x+4y-2=0的最短距离为（ ）A．9
B．8
C．5
D．2
【答案】分析：先求出圆心到直线的距离，再由圆与直线的位置关系得圆上的点M到直线的最小距离等于圆心到直线的距离减去圆的半径．
解答：解：由题意得圆的圆心为（5，3）
则圆心到直线3x+4y-2=0的距离为d=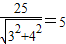
所以M点到直线3x+4y-2=0的最短距离为5-3=2，
故选D．
点评：解决此类题目的关键是熟悉直线与圆的位置关系，熟记点到直线的距离公式，然后准确的计算出最小距离．
解答：解：由题意得圆的圆心为（5，3）
则圆心到直线3x+4y-2=0的距离为d=
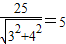
所以M点到直线3x+4y-2=0的最短距离为5-3=2，
故选D．
点评：解决此类题目的关键是熟悉直线与圆的位置关系，熟记点到直线的距离公式，然后准确的计算出最小距离．
练习册系列答案
寒假学与练系列答案
相关题目
点M在圆（x-5）2+（y-3）2=9上，则M点到直线3x+4y-2=0的最短距离为（ ）
| A、9 | B、8 | C、5 | D、2 |