题目内容
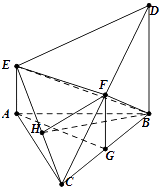
【题目】如图,在多面体ABCDE中,DB⊥平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,2AE=BD=2.
(Ⅰ)若F是线段CD的中点,证明:EF⊥面DBC;
(Ⅱ)求二面角D﹣EC﹣B的平面角的余弦值.
【答案】证明:(Ⅰ)取BC的中点G,连接FG,AG,
∵AG⊥BC,AG⊥BD,BD∩BC=B,
∴AG⊥面DBC,
又∵AE∥BD∥FG,AE=FG,
∴AGFE为平行四边形,
∴EF∥AG,∴EF⊥面DBC.
解:(Ⅱ)连接BF,过F在面DEC内作EC的垂线,垂足为H
连接HB.∵EF⊥面DBC,∴BF⊥EF,
又∵BC=BD,∴BF⊥CD,∴BF⊥面EDC,
∴∠FHB为二面角D﹣EC﹣B的平面角,
在△DEC中,∵ ![]() ,∴
,∴ ![]() ,
,
在直角△BFH中, ![]() ,
, ![]() ,
, ![]() ,
,
∴cos∠FHB= ![]() =
= ![]() .
.
∴二面角D﹣EC﹣B的平面角的余弦值为 ![]() .
.
【解析】(Ⅰ)取BC的中点G,连接FG,AG,推导出AG⊥面DBC,AGFE为平行四边形,由此能证明EF⊥面DBC.(Ⅱ)连接BF,过F在面DEC内作EC的垂线,垂足为H,连接HB,则∠FHB为二面角D﹣EC﹣B的平面角,由此能求出二面角D﹣EC﹣B的平面角的余弦值.
【考点精析】掌握直线与平面垂直的判定是解答本题的根本,需要知道一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.

【题目】已知下表为函数![]() 部分自変量取值及其对应函数值,为了便于研究,相关函数值取非整数值时,取值精确到0.01.
部分自変量取值及其对应函数值,为了便于研究,相关函数值取非整数值时,取值精确到0.01.
| 0.61 | -0.59 | -0.56 | -0.35 | 0 | 0.26 | 0.42 | 1.57 | 3.27 |
| 0.07 | 0.02 | -0.03 | -0.22 | 0 | 0.21 | 0.20 | -10.04 | -101.63 |
据表中数据,研究该函数的一些性质;
(1)判断函数![]() 的奇偶性,并证明;
的奇偶性,并证明;
(2)判断函数![]() 在区间[0.55,0.6]上是否存在零点,并说明理由;
在区间[0.55,0.6]上是否存在零点,并说明理由;
(3)判断![]() 的正负,并证明函数
的正负,并证明函数![]() 在
在![]() 上是单调递减函数.
上是单调递减函数.


