题目内容
9.设x、y、z是三个不全为零的实数,求$\frac{xy+2yz}{{x}^{2}+{y}^{2}+{z}^{2}}$的最大值为$\frac{\sqrt{5}}{2}$.分析 由于求的是最大值,可设x,y,z>0,由x2+my2≥2$\sqrt{m}$xy,(0<m<1,x=$\sqrt{m}$y取得等号),由(1-m)y2+z2≥2$\sqrt{1-m}$yz(z=$\sqrt{1-m}$y取得等号),当2$\sqrt{m}$=$\sqrt{1-m}$即m=$\frac{1}{5}$时,对分母运用基本不等式,化简整理,即可得到最大值为$\frac{\sqrt{5}}{2}$.
解答 解:由于求的是最大值,可设x,y,z>0,
由x2+my2≥2$\sqrt{m}$xy,(0<m<1,x=$\sqrt{m}$y取得等号),
由(1-m)y2+z2≥2$\sqrt{1-m}$yz(z=$\sqrt{1-m}$y取得等号),
当2$\sqrt{m}$=$\sqrt{1-m}$即m=$\frac{1}{5}$时,
$\frac{xy+2yz}{{x}^{2}+{y}^{2}+{z}^{2}}$=$\frac{xy+2yz}{({x}^{2}+\frac{1}{5}{y}^{2})+(\frac{4}{5}{y}^{2}+{z}^{2})}$≤$\frac{xy+2yz}{\frac{2\sqrt{5}}{5}xy+\frac{4\sqrt{5}}{5}yz}$
=$\frac{5}{2\sqrt{5}}$=$\frac{\sqrt{5}}{2}$.
当且仅当2x=$\frac{2\sqrt{5}}{5}$y=z时,取得最大值,且为$\frac{\sqrt{5}}{2}$.
故答案为:$\frac{\sqrt{5}}{2}$.
点评 本题考查基本不等式的运用:求最值,运用待定系数法求得m,是解题的关键,属于中档题.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
1. 我校高二期中考试统一测试文科的数学成绩分组统计如下表:
我校高二期中考试统一测试文科的数学成绩分组统计如下表:
(Ⅰ)求出表中m、n、M、N的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;
(Ⅱ)若我校参加本次考试的文科学生有600人,试估计这次测试中我校成绩在90分以上的人数;
(Ⅲ)若我校教师拟从分数不超过60分的学生中选取2人进行个案分析,求被选中2人分数不超过30分的概率.
 我校高二期中考试统一测试文科的数学成绩分组统计如下表:
我校高二期中考试统一测试文科的数学成绩分组统计如下表:(Ⅰ)求出表中m、n、M、N的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;
| 分组 | 频数 | 频率 |
| (0,30] | 3 | 0.03 |
| (30,60] | 3 | 0.03 |
| (60,90] | 37 | 0.37 |
| (90,120] | m | n |
| (120,150] | 15 | 0.15 |
| 合计 | M | N |
(Ⅲ)若我校教师拟从分数不超过60分的学生中选取2人进行个案分析,求被选中2人分数不超过30分的概率.
19.从某学校高三年级800名学生中随机抽取50名测量身高,据测量,被抽取学生的身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组方法得到的条形图.
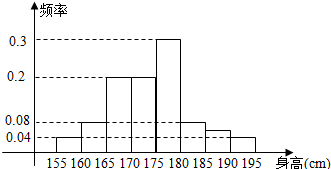
(1)根据已知条件填写下面表格:
(2)估计这所学校高三年级800名学生中身高在175cm以上(含175cm)的人数;
(3)在样本中,若第二组有1人为男生,其余为女生,第七组有1人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为同性别学生的概率是多少?

(1)根据已知条件填写下面表格:
| 组别 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 频数 |
(3)在样本中,若第二组有1人为男生,其余为女生,第七组有1人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为同性别学生的概率是多少?
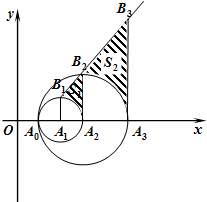 如图,在平面直角坐标系xOy中,设a1=2,有一组圆心在x轴正半轴上的圆An(n=1,2,…)与x轴的交点分别为A0(1,0)和An+1(an+1,0).过圆心An作垂直于x轴的直线ln,在第一象限与圆An交于点Bn(an,bn).
如图,在平面直角坐标系xOy中,设a1=2,有一组圆心在x轴正半轴上的圆An(n=1,2,…)与x轴的交点分别为A0(1,0)和An+1(an+1,0).过圆心An作垂直于x轴的直线ln,在第一象限与圆An交于点Bn(an,bn). 如图,矩形纸片ABCD的周长为l,面积为S.
如图,矩形纸片ABCD的周长为l,面积为S.