题目内容
已知两点M和N分别在直线y=mx和y=-mx(m>0)上运动,且|MN|=2,动点P满足:2![]() =
=![]() +
+![]() (O为坐标原点),点P的轨迹记为曲线C.
(O为坐标原点),点P的轨迹记为曲线C.
(1)求曲线C的方程,并讨论曲线C的类型;
(2)过点(0,1)作直线l与曲线C交于不同的两点A、B,若对于任意m>1,都有∠AOB为锐角,求直线l的![]() 斜率k的取值范围.
斜率k的取值范围.
(1)由2![]() =
=![]() +
+![]() ,得P是MN的中点.
,得P是MN的中点.
设P(x,y),M(x1,mx1),N(x2,-mx2),依题意得:
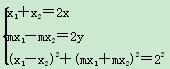 ,
,
消去x1,x2,整理得![]() +
+![]() =1.
=1.
当m>1时,方程表示焦点在y轴上的椭圆;
当0<m<1时,方程表示焦点在x轴上的椭圆;
当m=1时,方程表示圆.
(2)由m>1知方程表示焦点在y轴上的椭圆,直线l与曲线C恒有两交点,直线斜率不存在时不符合题意.
可设直线l的方程为y=kx+1,
直线与椭圆交点A(x3,y3),B(![]() x4,y4).
x4,y4).
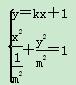 ⇒(m4+k2)x2+2kx+1-m2=0.
⇒(m4+k2)x2+2kx+1-m2=0.
x3+x4=-![]() ,x3x4=
,x3x4=![]() .
.
y3y4=(kx3+1)(kx4+1)=![]() +
+![]() +1.
+1.
要使∠AOB为锐角,只需![]() ·
·![]() >0,
>0,
∴x3x4+y3y4=![]() >0.
>0.
即m4-(k2+1)m2+1>0,可得m2+![]() >k2+1,
>k2+1,
对于任意m>1恒成立.
而m2+![]() >2,∴k2+1≤2,-1≤k≤1.
>2,∴k2+1≤2,-1≤k≤1.
所以k的取值范围是[-1,1].

练习册系列答案
相关题目
 (O为坐标原点),点P的轨迹记为曲线C.
(O为坐标原点),点P的轨迹记为曲线C. (O为坐标原点),点P的轨迹记为曲线C.
(O为坐标原点),点P的轨迹记为曲线C. (O为坐标原点),点P的轨迹记为曲线C.
(O为坐标原点),点P的轨迹记为曲线C.