题目内容
如图,正方体ABCD-A1B1C1D1的棱长为1,O是底面A1B1C1D1的中心,则点O到平面ABC1D1的距离为 .
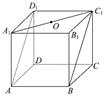


以D为原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系如图所示,

则A(1,0,0),B(1,1,0),D1(0,0,1),C1(0,1,1),O( ,
, ,1),
,1),
 =(0,1,0),
=(0,1,0), =(-1,0,1),
=(-1,0,1),
设平面ABC1D1的法向量n=(x,y,z),
由
得
令x=1,得n=(1,0,1).
又 =(-
=(- ,-
,- ,0),
,0),
∴O到平面ABC1D1的距离d= =
= =
= .
.

则A(1,0,0),B(1,1,0),D1(0,0,1),C1(0,1,1),O(
 ,
, ,1),
,1), =(0,1,0),
=(0,1,0), =(-1,0,1),
=(-1,0,1),设平面ABC1D1的法向量n=(x,y,z),
由

得

令x=1,得n=(1,0,1).
又
 =(-
=(- ,-
,- ,0),
,0),∴O到平面ABC1D1的距离d=
 =
= =
= .
.
练习册系列答案
相关题目
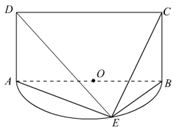
 是以
是以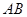 为直径的半圆
为直径的半圆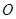 上异于
上异于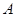 、
、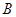 的点,矩形
的点,矩形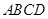 所在的平面垂直于半圆
所在的平面垂直于半圆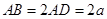 .
.
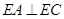 ;
;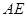 和
和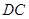 所成的角为
所成的角为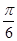 ,求平面
,求平面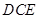 与平面
与平面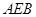 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.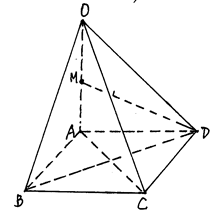
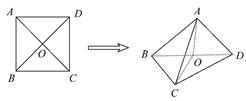
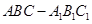 (侧棱和底面垂直的棱柱)中,
(侧棱和底面垂直的棱柱)中,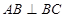 ,
,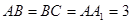 ,
,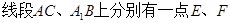 ,且满足
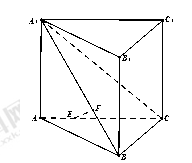
,且满足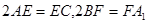 .
.
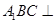 侧面
侧面 ;
; 的平面角的余弦值。
的平面角的余弦值。 ,2),则m= .
,2),则m= .
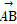 与
与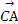 的夹角θ的大小是( )
的夹角θ的大小是( )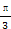
 π
π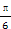
 π
π