题目内容
f（x）=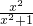
，f（2）+f（
）+f（3）+
+…+f（2012）+
=________．
解：∵f（x）=，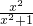
∴f（
）=
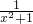
∴f（x）+f（）=1
∴f（2）+f（）+f（3）++…+f（2012）+=2011
故答案为：2011
分析：由已知中f（x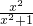）=，我们可以求出f（x）+f（）=1，然后利用分组分解法即可求出答案．
点评：本题考查的知识点是函数的值，其中根据已知得到f（x）+f（）=1，是解答本题的关键，本题易忽略是从2开始到2012，共2011组，而错认为是从1开始的，而错解为2012．
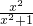，∴f（
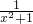
）=∴f（x）+f（
）=1∴f（2）+f（
）+f（3）++…+f（2012）+=2011故答案为：2011
分析：由已知中f（x）=
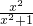，我们可以求出f（x）+f（）=1，然后利用分组分解法即可求出答案．点评：本题考查的知识点是函数的值，其中根据已知得到f（x）+f（
）=1，是解答本题的关键，本题易忽略是从2开始到2012，共2011组，而错认为是从1开始的，而错解为2012． 
练习册系列答案
提分百分百检测卷系列答案
相关题目