题目内容
【题目】已知抛物线
.
（1）若过点
作与抛物线相交的弦，要使其弦长为2的弦有几条？并说明理由.
（2）试研究过点
，且使弦长为2的弦有几条？并说明理由.
【答案】（1）只有一条，理由见解析；（2）当
时，有两条；当
时，有一条；当
时，不存在；理由见解析
【解析】
设过点
的直线为
，联立
，弦长公式
；
（1）时，代入即可求解；
（2）
时，利用弦长公式建立关于
的方程，转化成讨论方程根的情况即可求解.
解：设过点的直线为，
设直线与
交于
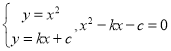，则
（1），
，
，
， 
所以过点
弦长为2的弦有1条，该弦所在直线为
.
（2）时，
，
则
.
，
令
，则
有非负实根
恒成立，即方程必然有解，
又因为
，
要存在非负实根，
当时，
，则，只有一条；
当时，
，则
有两个不等值，有两条；
综上所述，
当时，有两条；当时，只有一条；当时，不存在.
【题目】为了解人们对于国家新颁布的“生育二胎放开”政策的热度，现在某市进行调查，随机调查了
人，他们年龄的频数分布及支持“生育二胎”人数如下表：
年龄 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
支持“生 育二胎” | 4 | 5 | 12 | 8 | 2 | 1 |
（1）由以上统计数据填下面2乘2列联表，并问是否有99
的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异：
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
支持 | a= | c= | |
不支持 | b= | d= | |
合计 |
（2）若对年龄在
的被调查人中随机选取两人进行调查，恰好这两人都支持“生育二胎放开”的概率是多少？
参考数据：P
【题目】2018年双11当天，某购物平台的销售业绩高达2135亿人民币．与此同时，相关管理部门推出了针对电商的商品和服务的评价体系，现从评价系统中选出200次成功交易，并对其评价进行统计，对商品的好评率为0.9，对服务的好评率为0.75，其中对商品和服务都做出好评的交易为140次．
（1）请完成下表，并判断是否可以在犯错误概率不超过0.5％的前提下，认为商品好评与服务好评有关？
对服务好评 | 对服务不满意 | 合计 | |
对商品好评 | 140 | ||
对商品不满意 | 10 | ||
合计 | 200 |
（2）若针对服务的好评率，采用分层抽样的方式从这200次交易中取出4次交易，并从中选择两次交易进行客户回访，求只有一次好评的概率．
附：
，其中n＝a＋b＋c＋d．
P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
