题目内容
是否存在非零常数a、b、p,使得抛物线C1: y=ax2+bx与抛物线C2:y2=2px(p>0)关于直线x+y=1对称?若存在,求出a、b、p的值;若不存在,请说明理由.
解:假设存在常数a、b、p,使得原命题成立.
点(0,0)为抛物线C2的顶点,(0,0)关于直线:x+y=1的对称点为(1,1),而(1,1)为抛物线C1:y=ax2+bx的顶点.
又∵y=ax2+bx=a(x+![]() )2-
)2-![]() ,
,
∴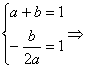 a=-1,b=2.
a=-1,b=2.
又∵点(0,0)在抛物线C1上,它关于直线x+y=1的对称点(1,1)在抛物线C2上,
代入解得p=![]() .
.
故存在非零常数a、b、p,a=-1,b=2,p=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
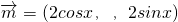 ,
,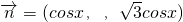 ,函数
,函数 (a、b为常数且x∈R).
(a、b为常数且x∈R). 时,f(x)的值域为[2,8].若存在,求出a、b的值;若不存在,说明理由.
时,f(x)的值域为[2,8].若存在,求出a、b的值;若不存在,说明理由. ,
, ,函数
,函数 (a、b为常数且x∈R).
(a、b为常数且x∈R). 时,f(x)的值域为[2,8].若存在,求出a、b的值;若不存在,说明理由.
时,f(x)的值域为[2,8].若存在,求出a、b的值;若不存在,说明理由.