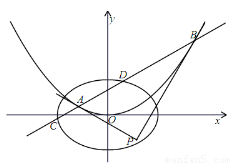
题目内容
抛物线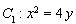 在点
在点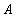 ,
,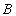 处的切线垂直相交于点
处的切线垂直相交于点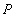 ,直线
,直线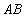 与椭圆
与椭圆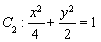 相交于
相交于 ,
, 两点.
两点.
(1)求抛物线 的焦点
的焦点 与椭圆
与椭圆 的左焦点
的左焦点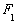 的距离;
的距离;
(2)设点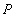 到直线
到直线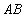 的距离为
的距离为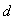 ,试问:是否存在直线
,试问:是否存在直线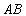 ,使得
,使得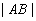 ,
,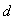 ,
,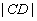 成等比数列?若存在,求直线
成等比数列?若存在,求直线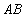 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
【答案】
(1)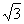 ;(2)不存在.
;(2)不存在.
【解析】
试题分析:(1)分别求出抛物线与椭圆的焦点,利用两点间距离公式求解;(2)设直线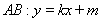 与抛物线相交于
与抛物线相交于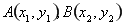 与椭圆相交于
与椭圆相交于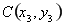 ,
,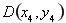 ,所以直线与抛物线方程联立,得到
,所以直线与抛物线方程联立,得到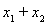 和
和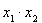 然后利用
然后利用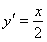 ,求出切线
,求出切线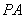 ,
,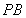 的斜率,利用切线垂直,
的斜率,利用切线垂直,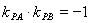 ,解出m,然后分别设出过
,解出m,然后分别设出过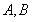 点的切线方程,求出交点
点的切线方程,求出交点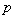 的坐标,利用点到直线的距离公式求
的坐标,利用点到直线的距离公式求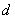 ,直线与曲线相交的弦长公式求
,直线与曲线相交的弦长公式求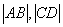 ,若
,若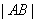 ,
,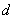 ,
,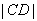 成等比数列,则
成等比数列,则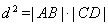 ,化简等式,通过
,化简等式,通过 看方程实根情况.
看方程实根情况.
试题解析:(I)抛物线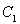 的焦点
的焦点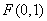 , 1分
, 1分
椭圆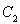 的左焦点
的左焦点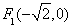 , 2分
, 2分
则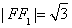 . 3分
. 3分
(II)设直线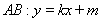 ,
,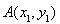 ,
,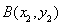 ,
,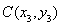 ,
,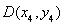 ,
,
由 ,得
,得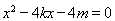 , 4分
, 4分
故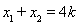 ,
,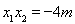 .
.
由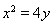 ,得
,得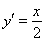 ,
,
故切线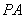 ,
,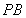 的斜率分别为
的斜率分别为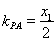 ,
,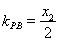 ,
,
再由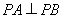 ,得
,得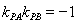 ,
,
即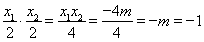 ,
,
故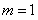 ,这说明直线
,这说明直线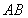 过抛物线
过抛物线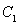 的焦点
的焦点 . 7分
. 7分
由 ,得
,得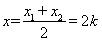 ,
,
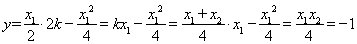 ,即
,即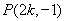 . 8分
. 8分
于是点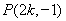 到直线
到直线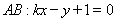 的距离
的距离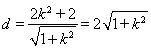 . 9分
. 9分
由 ,得
,得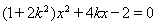 , 10分
, 10分
从而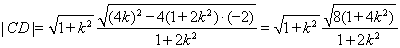 , 11分
, 11分
同理,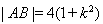 . 12分
. 12分
若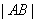 ,
,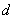 ,
,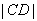 成等比数列,则
成等比数列,则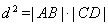 , 13分
, 13分
即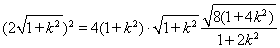 ,
,
化简整理,得 ,此方程无实根,
,此方程无实根,
所以不存在直线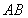 ,使得
,使得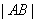 ,
,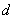 ,
,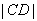 成等比数列. 15分
成等比数列. 15分
考点:1.椭圆与抛物线的性质;2.导数的几何意义;3.直线与曲线的交点问题;4.弦长公式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
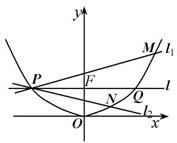 已知抛物线C:x2=2py(p为正常数)的焦点为F,过F做一直线l交C于P,Q两点,点O为坐标原点.
已知抛物线C:x2=2py(p为正常数)的焦点为F,过F做一直线l交C于P,Q两点,点O为坐标原点. 如图,圆C1:(x-a)2+y2=r2(r>0)与抛物线C2:x2=2py(p>0)的一个交点M(2,1),且抛物线在点M处的切线过圆心C1.
如图,圆C1:(x-a)2+y2=r2(r>0)与抛物线C2:x2=2py(p>0)的一个交点M(2,1),且抛物线在点M处的切线过圆心C1.