题目内容
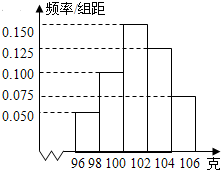某工厂对一批产品进行了抽样检测．如图是根据抽样检测后的产品净重（单位：克）数据绘制的频率分布直方图，其中产品净重的范围是[96，106]，样本数据分组为[96，98），[98，100），[100，102），[102，104），[104，106]，已知样本中产品净重小于100克的个数是36，则样本中净重大于或等于98克并且小于104克的产品的个数是（ ）| A、90 | B、75 | C、60 | D、45 |
分析：根据小长方形的面积=组距×
=频率求出频率，再根据频率=
求出频数，建立等式关系，解之即可．
| 频率 |
| 组距 |
| 频数 |
| 样本容量 |
解答：解：净重大于或等于98克并且小于104克的产品的个数设为N2，产品净重小于100克的个数设为N1=36，样本容量为N，则
=
=
，
N2=
×36=90
故选A．
| N2 |
| N1 |
| (0.1+0.15+0.125)×2×N |
| (0.05+0.1)×2×N |
| 375 |
| 150 |
N2=
| 375 |
| 150 |
故选A．
点评：用样本估计总体，是研究统计问题的一个基本思想方法．对于总体分布，总是用样本的频率分布对它进行估计，频率分布直方图：小长方形的面积=组距×
=频率，各个矩形面积之和等于1，频率=
，即f1=
，属于基础题．
| 频率 |
| 组距 |
| 频数 |
| 样本容量 |
| N1 |
| N |
练习册系列答案
阅读快车系列答案
相关题目
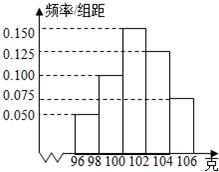某工厂对一批产品进行了抽样检测．右图是根据抽样检测后的产品净重（单位：克）数据绘制的频率分布直方图，其中产品净重的范围是[96，106]，样本数据分组为[96，98），[98，100），[100，102），[102，104），[104，106]，已知样本中产品净重小于100克的个数是36，则样本中净重大于或等于98克并且小于104克的产品的个数是
某工厂对一批产品进行了抽样检测，右图是根据抽样检测后的产品净重（单位：克）数据绘制的频率分布直方图，其中产品净重的范围是[96，106]，样本数据分组为[96，98），[98，100），[100，102），[102，104），[104，106]，已知样本中产品净重小于100克的个数是36．
（2013•闵行区二模）某工厂对一批产品进行抽样检测，根据抽样检测后的产品净重（单位：克）数据绘制的频率分布直方图如图所示，已知产品净重的范围是区间[96，106]，样本中净重在区间[96，100）的产品个数是24，则样本中净重在区间[100，104）的产品个数是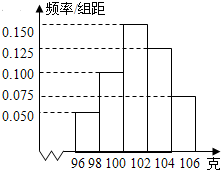
某工厂对一批产品进行了抽样检测，右图是根据抽样检测后的产品净重（单位：克）数据绘制的频率分布直方图，其中产品净重的范围是[96，106]，样本数据分组为[96，98），[98，100），[100，102），[102，104），[l04，l06]．已知样本中产品净重小于100克的个数是36，则样本中净重大于或等于98克并且小于102克的产品的个数是（ ）