题目内容
已知实数数列{an}中,a1=1,a6=32,an+2=
| ||
| an |
a1
a2a3a4
a5a6a7a8a9
(1)A(12,5)=
(2)若A(m,n)•A(n,m)=250,则m+n=
分析:(1)由题意知{an}是等比数列,且an=2n-1,第m行的最后一个数是am2,所以A(12,5)=a126=2125.
(2)A(m,n)•A(n,m)=a(m-1)2+n•a(n-1)2+m=2m2-2m+n•2n2-2n+m=250,所以m+n=11.
(2)A(m,n)•A(n,m)=a(m-1)2+n•a(n-1)2+m=2m2-2m+n•2n2-2n+m=250,所以m+n=11.
解答:解:(1)由题意知{an}是等比数列,且an=2n-1,第m行的最后一个数是am2,
∴A(12,5)=a112+5=a126=2125.
(2)A(m,n)•A(n,m)
=a(m-1)2+n•a(n-1)2+m
=2m2-2m+n•2n2-2n+m
=2m2+n2-m-n=250
∴m+n=11.
∴A(12,5)=a112+5=a126=2125.
(2)A(m,n)•A(n,m)
=a(m-1)2+n•a(n-1)2+m
=2m2-2m+n•2n2-2n+m
=2m2+n2-m-n=250
∴m+n=11.
点评:本题考查数列的性质和应用,解题时要认真审题,仔细解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
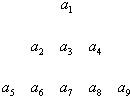
 已知实数数列{an}中,a1=1,a6=32,an+2=
已知实数数列{an}中,a1=1,a6=32,an+2=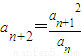 ,把数列{an}的各项排成如右图的三角形状.记A(m,n)为第m行从左起第n个数,则若A(m,n)•A(n,m)=250,则m+n= .
,把数列{an}的各项排成如右图的三角形状.记A(m,n)为第m行从左起第n个数,则若A(m,n)•A(n,m)=250,则m+n= .
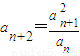 ,把数列{an}的各项排成如下图的三角形状、记A(m,n)为第m行从左起第n个数,则
,把数列{an}的各项排成如下图的三角形状、记A(m,n)为第m行从左起第n个数,则