Question

方程sin(x-

π

4

)=

1

4

x的实数解的个数是（　　）

A．0

B．1

C．2

D．3

Answer 1

分析：要求方程sin（x-

π

4

）=

1

4

x的实数解的个数，即求 y=sin（x-

π

4

），y=

1

4

x，这两个方程的曲线交点的个数就是原方程实数解的个数，根据直线 的斜率大小，和-1≤sin（x-

π

4

）≤1，以及三角函数的周期性，即可求得结论．

解答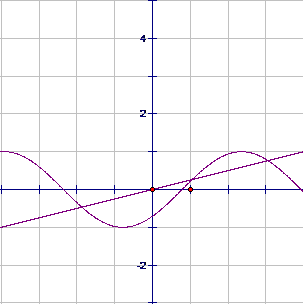：解：在同一个坐标系中作出y=sin（x-

π

4

） 和y=

1

4

x的图象，如图所示：
                        
由于y=sin（x-

π

4

） 和y=

1

4

x的图象有3个交点，方程sin(x-

π

4

)=

1

4

x的实数解的个数是3
故选D．

点评：本题考查根的存在性以及根的个数的判断，以及三角函数的周期性，正弦函数的图象特征，利用两曲线交点的个数判断方程的解的个数，体现了数形结合的数学思想，属于中档题．