题目内容
18．如图，给出了奇函数f（x）和偶函数g（x）的部分图象，根据图象求f（-3），g（2）的值．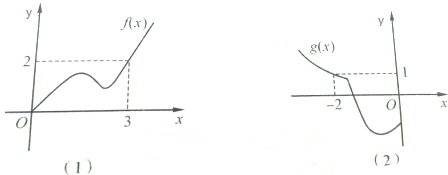
分析 利用图象，结合奇偶函数的定义，即可得出结论．
解答 解：∵函数f（x）是奇函数，∴f（-3）=-f（3）=-2；
∵函数g（x）是偶函数，∴g（2）=g（-2）=1．
点评 本题考查奇偶函数的定义，数形结合的数学思想，比较基础．
练习册系列答案
名校课堂系列答案
相关题目
9．已知a＞0，x0是函数y=ax-b的零点，则（ ）
| A． | 对任意x∈R，$\frac{1}{2}$ax2-bx≥$\frac{1}{2}$ax02-bx0恒成立 | |
| B． | 对任意x∈R，$\frac{1}{2}$ax2-bx≤$\frac{1}{2}$ax02-bx0恒成立 | |
| C． | 对任意x∈R，$\frac{1}{2}$ax2-bx＞$\frac{1}{2}$ax02-bx0恒成立 | |
| D． | 对任意x∈R，$\frac{1}{2}$ax2-bx与$\frac{1}{2}$ax02-bx0的大小关系不确定 |
7．已知数列{an}的前n项的“均倒数”为$\frac{1}{2n+1}$，又bn=$\frac{{a}_{n}+1}{4}$，则$\frac{1}{{b}_{1}{b}_{2}}$+$\frac{1}{{b}_{2}{b}_{3}}$+…+$\frac{1}{{b}_{10}{b}_{11}}$=（ ）
| A． | $\frac{1}{11}$ | B． | $\frac{1}{12}$ | C． | $\frac{10}{11}$ | D． | $\frac{11}{12}$ |