题目内容
【题目】已知边长为![]() 的等边三角形的一个顶点位于原点,另外两个顶点在抛物线
的等边三角形的一个顶点位于原点,另外两个顶点在抛物线![]() :
:![]() (
(![]() )上.
)上.
(1)求抛物线![]() 的方程;
的方程;
(2)直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,交抛物线
两点,交抛物线![]() 的准线
的准线![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,若
,若![]() .证明:直线
.证明:直线![]() 过定点,并求出定点坐标.
过定点,并求出定点坐标.
【答案】(1)![]() ;(2)证明见解析;定点
;(2)证明见解析;定点![]() .
.
【解析】
(1)利用抛物线的对称性,可知点![]() 在抛物线
在抛物线![]() 上,将点代入抛物线方程,求出
上,将点代入抛物线方程,求出![]() 值,进而得解;
值,进而得解;
(2先求出抛物线的准线方程,设出直线![]() 的方程,求出
的方程,求出![]() 点和
点和![]() 点坐标,设出
点坐标,设出![]() 点和
点和![]() 点坐标,联立直线
点坐标,联立直线![]() 的方程与抛物线方程,得到
的方程与抛物线方程,得到![]() ,
,![]() ,然后进行向量数量积的坐标运算,化简,并将韦达定理代入,可得
,然后进行向量数量积的坐标运算,化简,并将韦达定理代入,可得![]() ,求出
,求出![]() 的值,进而得解.
的值,进而得解.
(1)![]() ,
,
因为边长为![]() 的等边三角形的一个顶点位于原点,
的等边三角形的一个顶点位于原点,
另外两个顶点在抛物线![]() :
:![]() (
(![]() )上,
)上,
并且,该抛物线关于![]() 轴对称,
轴对称,
所以点![]() 在抛物线
在抛物线![]() 上,
上,
所以![]() ,解得
,解得![]() ,
,
所以抛物线![]() 的方程为
的方程为![]() .
.
(2)证明:由(1)得抛物线![]() 的准线的方程为
的准线的方程为![]() .
.
设直线![]() 的方程为
的方程为![]() (
(![]() ),
),
令![]() ,解得
,解得![]() ,所以
,所以![]() ,
,
![]() ,解得
,解得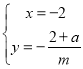 ,所以
,所以![]() ,
,
由得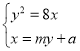 ,得
,得![]() ,其中
,其中![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]()
![]()
![]()
![]()
![]() .
.
由![]() ,得
,得![]() ,解得
,解得![]() ,
,
所以直线![]() 的方程为
的方程为![]() ,因此直线
,因此直线![]() 过定点
过定点![]() .
.

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案【题目】噪声污染已经成为影响人们身体健康和生活质量的严重问题,为了了解声音强度![]() (单位:分贝)与声音能量(单位:
(单位:分贝)与声音能量(单位:![]() )之间的关系,将测量得到的声音强度
)之间的关系,将测量得到的声音强度![]() 和声音能量
和声音能量![]() (
(![]() =1,2…,10)数据作了初步处理,得到如图散点图及一些统计量的值.
=1,2…,10)数据作了初步处理,得到如图散点图及一些统计量的值.

|
|
|
|
|
| 45.7 |
|
| 0.51 |
|
| |||
| 5.1 | |||
表中![]() ,
,![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为声音强度
哪一个适宜作为声音强度![]() 关于声音能量的回归方程类型?(给出判断即可,不必说明理由)
关于声音能量的回归方程类型?(给出判断即可,不必说明理由)
(2)根据表中数据,求声音强度![]() 关于声音能量的回归方程;
关于声音能量的回归方程;
(3)当声音强度大于60分贝时属于噪音,会产生噪音污染,城市中某点![]() 共受到两个声源的影响,这两个声源的声音能量分别是
共受到两个声源的影响,这两个声源的声音能量分别是![]() 和
和![]() ,且
,且![]() .己知点
.己知点![]() 的声音能量等于声音能量
的声音能量等于声音能量![]() 与
与![]() 之和.请根据(1)中的回归方程,判断
之和.请根据(1)中的回归方程,判断![]() 点是否受到噪音污染的干扰,并说明理由.
点是否受到噪音污染的干扰,并说明理由.
附:对于一组数据![]() .其回归直线
.其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: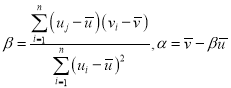 .
.
【题目】第23届冬季奥运会于2018年2月9日至2月25日在韩国平昌举行,期间正值我市学校放寒假,寒假结束后,某校工会对全校教职工在冬季奥运会期间每天收看比赛转播的时间作了一次调查,得到如下频数分布表:
收看时间(单位:小时) |
|
|
|
|
|
|
收看人数 | 14 | 30 | 16 | 28 | 20 | 12 |
(1)若将每天收看比赛转播时间不低于3小时的教职工定义为“体育达人”,否则定义为“非体育达人”,请根据频数分布表补全![]() 列联表:
列联表:
| 男 | 女 | 合计 |
体育达人 | 40 | ||
非体育达人 | 30 | ||
合计 |
并判断能否有![]() 的把握认为该校教职工是否为“体育达人”与“性别”有关;
的把握认为该校教职工是否为“体育达人”与“性别”有关;
(2)在全校“体育达人”中按性别分层抽样抽取6名,再从这6名“体育达人”中选取2名作冬奥会知识讲座.记其中女职工的人数为![]() ,求的
,求的![]() 分布列与数学期望.
分布列与数学期望.
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() .
.
