题目内容
上海某玩具厂生产x套吉祥物“福娃”所需成本费用为P元,且P=1000+5x+
x2,而每套售出的价格为Q元,其中Q=a+
(a,b∈R),
(1)问:该玩具厂生产多少套“福娃”时,使得每套“福娃”所需成本费用最少?
(2)若生产出的“福娃”能全部售出,且当产量为150套时利润最大,此时每套价格为30元,求a,b的值.(利润=销售收入-成本)
| 1 |
| 10 |
| x |
| b |
(1)问:该玩具厂生产多少套“福娃”时,使得每套“福娃”所需成本费用最少?
(2)若生产出的“福娃”能全部售出,且当产量为150套时利润最大,此时每套价格为30元,求a,b的值.(利润=销售收入-成本)
分析:(1)建立函数的解析式,再利用基本不等式求函数的最值;
(2)根据利润=销售收入-成本,求出利润函数Qx-P=x(a+
)-(1000+5x+
)=(
-
)x2+(a-5)x-1000,
再利用当产量为150套时利润最大,此时每套价格为30元,即可求a,b的值
(2)根据利润=销售收入-成本,求出利润函数Qx-P=x(a+
| x |
| b |
| x2 |
| 10 |
| 1 |
| b |
| 1 |
| 10 |
再利用当产量为150套时利润最大,此时每套价格为30元,即可求a,b的值
解答:解:(1)由题意,每套“福娃”所需成本费用为
=
=
x+
+5≥2
+5=25,
当
x=
,即x=100时,每套“福娃”所需成本费用最少为25元.(6分)
(2)利润为Qx-P=x(a+
)-(1000+5x+
)=(
-
)x2+(a-5)x-1000(9分).
由题意,
(12分)
解得 a=25,b=30.(14分).
| p |
| x |
1000+5x+
| ||
| x |
| 1 |
| 10 |
| 1000 |
| x |
| 100 |
当
| 1 |
| 10 |
| 1000 |
| x |
(2)利润为Qx-P=x(a+
| x |
| b |
| x2 |
| 10 |
| 1 |
| b |
| 1 |
| 10 |
由题意,
|
解得 a=25,b=30.(14分).
点评:本题考查函数模型的构建,考查利用基本不等式求函数的最值,考查二次函数的最值,确立函数模型是关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
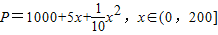 ,而每万套售出价格为Q元,其中
,而每万套售出价格为Q元,其中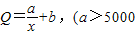 ,b>5),问:
,b>5),问: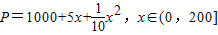 ,而每万套售出价格为Q元,其中
,而每万套售出价格为Q元,其中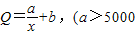 ,b>5),问:
,b>5),问: