题目内容
上海某玩具厂生产x万套世博会吉祥物海宝所需成本费用为P元，且P=1000+5x+
x2，x∈(0，200]，而每万套售出价格为Q元，其中Q=
+b，(a＞5000，b＞5），问：
（1）该玩具厂生产多少万套吉祥物时，使得每万套成本费用最低？
（2）若产出的吉祥物能全部售出，问产量多大时，厂家所获利润最大？
| 1 |
| 10 |
| a |
| x |
（1）该玩具厂生产多少万套吉祥物时，使得每万套成本费用最低？
（2）若产出的吉祥物能全部售出，问产量多大时，厂家所获利润最大？
分析：（1）
=
=
+
+5≥25（当且仅当x=100时，取等号），由此能求出该玩具厂生产多少万套吉祥物时，使得每万套成本费用最低．
（2）利润f(x)=(
+b)x-(1000+5x+
x2)=-
x2+(b-5)x+a-1000，x∈（0，200]，由此能求出厂家所获利润最大时的产量．
| P |
| x |
1000+5x+
| ||
| x |
| 1000 |
| x |
| x |
| 10 |
（2）利润f(x)=(
| a |
| x |
| 1 |
| 10 |
| 1 |
| 10 |
解答：解：（1）由题设知：
=
（3分）
=
+
+5≥25（当且仅当x=100时，取等号）
∴生产100万套时，每万套成本费用最低．（6分）
（2）由题设，利润f(x)=(
+b)x-(1000+5x+
x2)=-
x2+(b-5)x+a-1000，x∈（0，200]（9分）
当5（b-5）≤200，即b≤45时，
fmax(x)=f[5(b-5)]=
(b-5)2+a-1000
∴当产量为5b-25万套时，利润最大（12分）
当b＞45时，函数f（x）在（0，200]上是增函数，
∴当产量为200万套时，fmax（x）=200b+a-6000．（14分）
| P |
| x |
1000+5x+
| ||
| x |
=
| 1000 |
| x |
| x |
| 10 |
∴生产100万套时，每万套成本费用最低．（6分）
（2）由题设，利润f(x)=(
| a |
| x |
| 1 |
| 10 |
| 1 |
| 10 |
当5（b-5）≤200，即b≤45时，
fmax(x)=f[5(b-5)]=
| 5 |
| 2 |
∴当产量为5b-25万套时，利润最大（12分）
当b＞45时，函数f（x）在（0，200]上是增函数，
∴当产量为200万套时，fmax（x）=200b+a-6000．（14分）
点评：本题考查函数在生产实际中的应用，解题时要认真审题，仔细分析数量间的相互关系，合理地选择数学模型进行解题．
练习册系列答案
相关题目
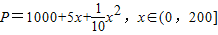，而每万套售出价格为Q元，其中
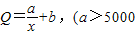，b＞5），问：
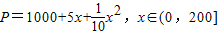，而每万套售出价格为Q元，其中
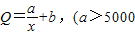，b＞5），问：
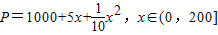，而每万套售出价格为Q元，其中
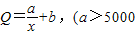，b＞5），问：
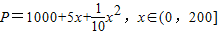，而每万套售出价格为Q元，其中
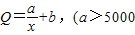，b＞5），问：