题目内容
(本小题共16分)已知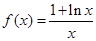 .
.
(1)若函数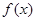 在区间
在区间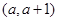 上有极值,求实数
上有极值,求实数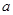 的取值范围;
的取值范围;
(2)若关于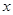 的方程
的方程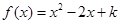 有实数解,求实数
有实数解,求实数 的取值范围;
的取值范围;
(3)当 ,
,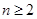 时,求证:
时,求证: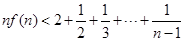 .
.
【答案】
解:(1)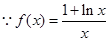 ,
,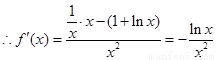
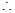 当
当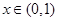 时,
时,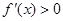 ;当
;当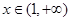 时,
时,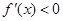 ;
;
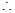 函数
函数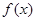 在区间(0,1)上为增函数;在区间
在区间(0,1)上为增函数;在区间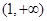 为减函数 -------------------------3分
为减函数 -------------------------3分
 当
当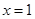 时,函数
时,函数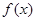 取得极大值,而函数
取得极大值,而函数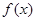 在区间
在区间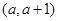 有极值.
有极值.
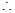
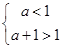 ,解得
,解得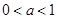 .
---------------------------5分
.
---------------------------5分
(2)由(1)得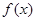 的极大值为
的极大值为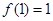 ,令
,令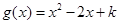 ,所以当
,所以当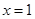 时,函数
时,函数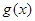 取得最小值
取得最小值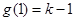 ,又因为方程
,又因为方程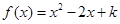 有实数解,那么
有实数解,那么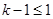 ,即
,即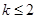 ,所以实数
,所以实数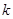 的取值范围是:
的取值范围是: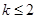 .
----------10分
.
----------10分
(另解: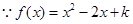 ,
,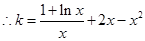 ,
,
令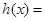
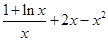 ,所以
,所以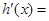
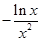
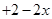 ,当
,当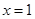 时,
时,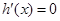
当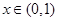 时,
时,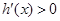 ;当
;当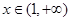 时,
时,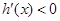
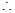 当
当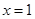 时,函数
时,函数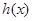 取得极大值为
取得极大值为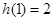
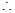 当方程
当方程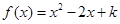 有实数解时,
有实数解时,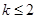 .)
.)
(3)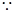 函数
函数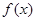 在区间
在区间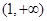 为减函数,而
为减函数,而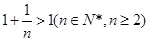 ,
,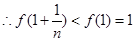
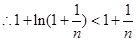 ,即
,即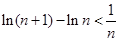
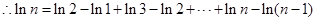
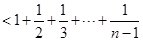 --------------12分
--------------12分
即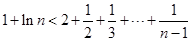 ,而
,而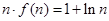 ,
,
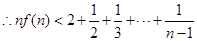 结论成立.
----------------------16分
结论成立.
----------------------16分
【解析】略

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目

 在直线
在直线 上.
上. 截得的弦长为2的圆的方程;
截得的弦长为2的圆的方程;