题目内容
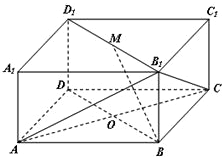 如图所示的长方体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,O为AC与BD的交点,BB1=
如图所示的长方体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,O为AC与BD的交点,BB1=| 2 |
(Ⅰ)求证:BM∥平面D1AC;
(Ⅱ)求证:D1O⊥平面AB1C;
(Ⅲ)求二面角B-AB1-C的大小.
分析:(Ⅰ)连接D1O,通过证明D1O∥BM,去证BM∥平面D1AC.
(Ⅱ通过证明 OB1⊥D1O.AC⊥D1O,由线面垂直的判定定理去证D1O⊥平面AB1C,
(Ⅲ)在平面ABB1中过点B作BE⊥AB1于E,连接EC,证明∠BEC是二面角B-AB1-C的平面角,再再直角三角形BEC中求解.
(Ⅱ通过证明 OB1⊥D1O.AC⊥D1O,由线面垂直的判定定理去证D1O⊥平面AB1C,
(Ⅲ)在平面ABB1中过点B作BE⊥AB1于E,连接EC,证明∠BEC是二面角B-AB1-C的平面角,再再直角三角形BEC中求解.
解答:解:(Ⅰ)连接D1O,如图,∵O、M分别是BD、B1D1的中点,BD1D1B是矩形,
∴四边形D1OBM是平行四边形,∴D1O∥BM.
∵D1O?平面D1AC,BM?平面D1AC,
∴BM∥平面D1AC.
(Ⅱ)连接OB1,∵正方形ABCD的边长为2,BB1=
,
∴B1D1=2
,OB1=2,D1O=2,
则OB12+D1O2=B1D12,∴OB1⊥D1O.
∵在长方体ABCD-A1B1C1D1中,AC⊥BD,AC⊥D1D,
∴AC⊥平面BDD1B1,又D1O?平面BDD1B1,
∴AC⊥D1O,又AC∩OB1=O,
∴D1O⊥平面AB1C.
(Ⅲ)在平面ABB1中过点B作BE⊥AB1于E,连接EC,
∵CB⊥AB,CB⊥BB1,
∴CB⊥平面ABB1,又AB1?平面ABB1,
∴CB⊥AB1,又BE⊥AB1,且CB∩BE=B,
∴AB1⊥平面EBC,而EC?平面EBC,
∴AB1⊥EC.
∴∠BEC是二面角B-AB1-C的平面角.
在Rt△BEC中,BE=
,BC=2
∴tan∠BEC=
,∠BEC=60°,
∴二面角B-AB1-C的大小为60°.
∴四边形D1OBM是平行四边形,∴D1O∥BM.
∵D1O?平面D1AC,BM?平面D1AC,
∴BM∥平面D1AC.
(Ⅱ)连接OB1,∵正方形ABCD的边长为2,BB1=
| 2 |
∴B1D1=2
| 2 |
则OB12+D1O2=B1D12,∴OB1⊥D1O.
∵在长方体ABCD-A1B1C1D1中,AC⊥BD,AC⊥D1D,
∴AC⊥平面BDD1B1,又D1O?平面BDD1B1,
∴AC⊥D1O,又AC∩OB1=O,
∴D1O⊥平面AB1C.
(Ⅲ)在平面ABB1中过点B作BE⊥AB1于E,连接EC,
∵CB⊥AB,CB⊥BB1,
∴CB⊥平面ABB1,又AB1?平面ABB1,
∴CB⊥AB1,又BE⊥AB1,且CB∩BE=B,
∴AB1⊥平面EBC,而EC?平面EBC,
∴AB1⊥EC.
∴∠BEC是二面角B-AB1-C的平面角.
在Rt△BEC中,BE=
2
| ||
| 3 |
∴tan∠BEC=
| 3 |
∴二面角B-AB1-C的大小为60°.
点评:本题考查直线和平面位置关系及其判定,二面角求解,考查转化的思想方法(线线位置关系转化为线面位置关系)空间想象能力,计算能力.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
 如图所示的长方体ABCD-A1B1C1D1中AB=BB1且BC=2AB,E,F分别是BC1,A1D1的中点,则异面直线BE与DF所成的角是
如图所示的长方体ABCD-A1B1C1D1中AB=BB1且BC=2AB,E,F分别是BC1,A1D1的中点,则异面直线BE与DF所成的角是
 ,
, =
= ,则二面角
,则二面角 的大小为_______;
的大小为_______;
 ,
, =
= ,二面角
,二面角 的大小为
▲ .
的大小为
▲ .
