题目内容
函数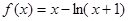 ,数列
,数列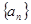 ,满足0<
,满足0<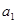 <1,
<1,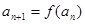 ,数列
,数列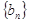 满足
满足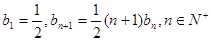 ,
,
(Ⅰ)求函数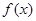 的单调区间;
的单调区间;
(Ⅱ)求证:0<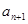 <
<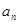 <1;
<1;
(Ⅲ)若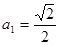 且
且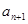 <
<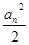 ,则当n≥2时,求证:
,则当n≥2时,求证: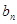 >
>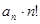
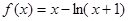 ,数列
,数列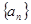 ,满足0<
,满足0<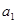 <1,
<1,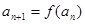 ,数列
,数列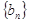 满足
满足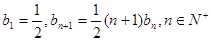 ,
,(Ⅰ)求函数
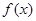 的单调区间;
的单调区间;(Ⅱ)求证:0<
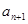 <
<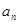 <1;
<1;(Ⅲ)若
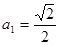 且
且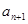 <
<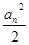 ,则当n≥2时,求证:
,则当n≥2时,求证: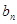 >
>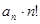
(Ⅰ)函数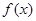 的递减区间(-1,0),递增区间(0,+
的递减区间(-1,0),递增区间(0,+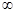 );(Ⅱ)详见解析;(Ⅲ)详见解析.
);(Ⅱ)详见解析;(Ⅲ)详见解析.
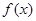 的递减区间(-1,0),递增区间(0,+
的递减区间(-1,0),递增区间(0,+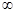 );(Ⅱ)详见解析;(Ⅲ)详见解析.
);(Ⅱ)详见解析;(Ⅲ)详见解析.试题分析:(Ⅰ)求函数
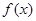 的单调区间,首先确定定义域
的单调区间,首先确定定义域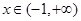 ,可通过单调性的定义,或求导确定单调区间,由于
,可通过单调性的定义,或求导确定单调区间,由于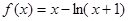 ,含有对数函数,可通过求导来确定单调区间,对函数
,含有对数函数,可通过求导来确定单调区间,对函数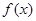 求导得
求导得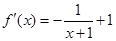 ,由此令
,由此令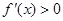 ,
,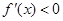 ,解出
,解出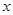 就能求出函数
就能求出函数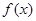 的单调区间;(Ⅱ)求证:0<
的单调区间;(Ⅱ)求证:0<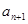 <
<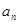 <1,可先证0<
<1,可先证0<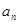 <1,
<1,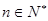 ,再证数列
,再证数列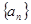 单调递减,可先证0<
单调递减,可先证0<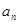 <1,若能求出通项公式,利用通项公式来证,由已知0<
<1,若能求出通项公式,利用通项公式来证,由已知0<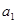 <1,
<1,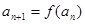 ,显然无法求通项公式,可考虑利用数学归纳法来证,结合函数
,显然无法求通项公式,可考虑利用数学归纳法来证,结合函数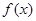 的单调性易证,证数列
的单调性易证,证数列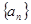 单调递减,可用作差比较法
单调递减,可用作差比较法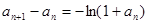 <0证得,从而的结论;(Ⅲ)若
<0证得,从而的结论;(Ⅲ)若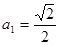 且
且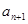 <
<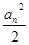 ,则当n≥2时,求证:
,则当n≥2时,求证: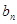 >
>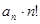 ,关键是求
,关键是求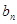 的通项公式,由
的通项公式,由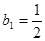 ,
,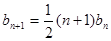 ,所以
,所以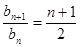 ,可得
,可得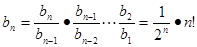 ,只要证明
,只要证明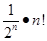 >
>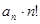 ,,即证
,,即证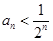 ,因为
,因为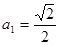 且
且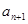 <
<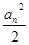 ,则
,则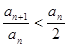 ,由此可得
,由此可得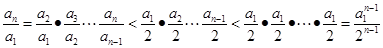 ,所以
,所以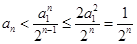 ,即证得.
,即证得.试题解析:(Ⅰ)利用导数可求得函数
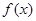 的递减区间(-1,0),递增区间(0,+
的递减区间(-1,0),递增区间(0,+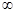 )
)(Ⅱ)先用数学归纳法证明0<
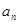 <1,
<1,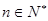 .
.①当n=1时,由已知得结论成立.②假设
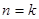 时,0<
时,0<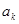 <1成立.则当
<1成立.则当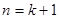 时由(1)可得函数
时由(1)可得函数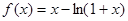 在
在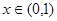 上是增函数,所以
上是增函数,所以
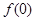 <
<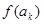 <
<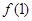 =1-
=1-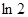 <1,所以0<
<1,所以0<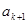 <1,即n=k+1时命题成立,由①②可得0<
<1,即n=k+1时命题成立,由①②可得0<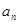 <1,
<1,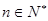 成立.
成立.又
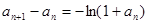 <0,所以
<0,所以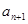 <
<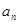 成立.
成立.所以0<
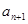 <
<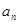 <1
<1(Ⅲ)因为
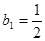 ,
,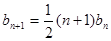 ,所以
,所以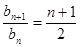 ,
,所以
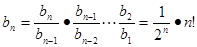 ……①
……①因为
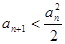 则
则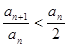 ,所以
,所以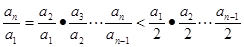
因为
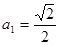 ,当
,当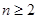 时,
时,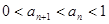 ,
,所以
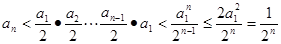 ……②
……②由①②两式可知
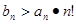

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
 ,(其中常数
,(其中常数 ).
). 时,求
时,求 的极大值;
的极大值; 上的单调性;
上的单调性; 时,曲线
时,曲线 上总存在相异两点
上总存在相异两点 、
、 ,使得曲线
,使得曲线 、
、 处的切线互相平行,求
处的切线互相平行,求 的取值范围.
的取值范围.  (
(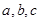 为常数)的图象过原点,且对任意
为常数)的图象过原点,且对任意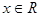 总有
总有 成立;
成立; 的最大值等于1,求
的最大值等于1,求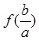 与
与 的大小关系.
的大小关系.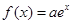 ,
,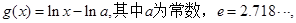 且
且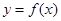
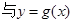 的图象在它们与坐标轴交点处的切线互相平行.
的图象在它们与坐标轴交点处的切线互相平行.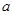 的值;
的值;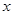 使不等式
使不等式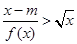 成立,求实数
成立,求实数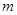 的取值范围;
的取值范围;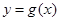 公共定义域内的任意实数
公共定义域内的任意实数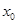 ,我们把
,我们把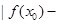
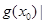 的值称为两函数在
的值称为两函数在 的一个焦点是
的一个焦点是 ,一条渐近线的方程是
,一条渐近线的方程是 .
. 为斜率的直线
为斜率的直线 与双曲线
与双曲线 ,且线段
,且线段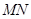 的垂直平分线与两坐标轴围成的三角形的面积为
的垂直平分线与两坐标轴围成的三角形的面积为 ,求
,求 的取值范围.
的取值范围. .
. 时,求函数
时,求函数 的最大值;
的最大值; 其图象上任意一点
其图象上任意一点 处切线的斜率
处切线的斜率 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,
, ,方程
,方程 有唯一实数解,求正数
有唯一实数解,求正数 的值.
的值. .
. 时,求函数
时,求函数 的极值;
的极值; ,使函数
,使函数 在
在 上有唯一的零点,若有,请求出
上有唯一的零点,若有,请求出 的范围;若没有,请说明理由.
的范围;若没有,请说明理由. 为函数
为函数 的导函数,则下列结论中正确的是( )
的导函数,则下列结论中正确的是( ) 且
且 ,
,




 ,给出定义:
,给出定义: 是函数
是函数 的导函数,
的导函数, 是
是 有实数解
有实数解 ,则称点
,则称点 为函数
为函数 的“拐点”。某同学经研究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且拐点就是对称中心。若
的“拐点”。某同学经研究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且拐点就是对称中心。若 ,请你根据这一发现,求:(1)函数
,请你根据这一发现,求:(1)函数 =________.
=________.