Question

给出下列命题：①分别和两条异面直线AB、CD同时相交的两条直线AC、BD一定是异面直线 ②同时与两条异面直线垂直的两直线不一定平行 ③斜线b在面α内的射影为c，直线a⊥c，则a⊥b ④异面直线a，b所成的角为60°，过空间一定点P，作直线L，使L与a，b 所成的角均为60°，这样的直线L有两条其中真命题是（ ）
A．①③
B．①
C．③④
D．②④

Answer 1

【答案】分析：用反证法证得①正确．②将其中一条异面直线平移与另一条相交确定一个平面，则二直线垂直同一个面，故这2条直线平行，故②不正确．③没有a在α内这个条件，不符合三垂线定理，故不正确．④这样的直线L有三条，故④不正确．
解答：解：①若AC、BD不异面，则ABCD共面，这与AB、CD异面矛盾，故①正确．
②将其中一条异面直线平移与另一条相交确定一个平面，则二直线垂直同一个面，故这2条直线平行，故②不正确．
③没有a在α内这个条件，不符合三垂线定理，故③不正确．
④这样的直线L有三条，
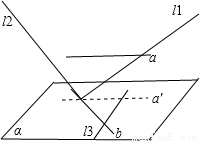
（如图所示：a∥a′，a′、b、l₃ 在平面α内，a，l₁，l₂在平面α 外，且l₁，l₂，l₃ 都满足条件） 
故④不正确，
故选B．

点评：本题主要考查异面直线判定方法，本题主要考查异面直线所成的角的定义，体现了数形结合的数学思想，属于基础题．