题目内容
不等式 的解集不是空集,则实数a的取值范围是( )
的解集不是空集,则实数a的取值范围是( )A.(0,+∞)
B.(1,+∞)
C.(-1,+∞)
D.(-∞,-1)
【答案】分析:首先得到不等式组的第二个不等式的解为:x>-a,然后分a的正负和a等于0的情况对第一个不等式的解加以讨论,可得当原不等式的解集不是空集时,实数a的取值范围.
解答:解:对于不等式组的第二个不等式:x+a>0,可以解得x>-a…①
(1)当a=0时,不等式第一个不等式为0>-1,解集为R,可得原不等式组解集不是空集,符合题意;
(2)当a>0时,不等式第一个不等式的解为:x>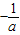 ,结合①可得交集不是空集,符合题意;
,结合①可得交集不是空集,符合题意;
(3)当a<0时,不等式第一个不等式的解为:x<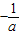 …②,
…②,
i.当a≤-1时,-a≥ ,对照①②可得不等式组的解集是空集;
,对照①②可得不等式组的解集是空集;
ii.当-1<a<0时,-a<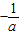 ,对照①②可得不等式组的解集是(-a,
,对照①②可得不等式组的解集是(-a,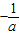 ),符合题意.
),符合题意.
综上所述,当原不等式的解集不是空集时,a>-1.
故选C
点评:本题以不等式的解集非空为例,考查了含有参数不等式的解法和集合关系中参数取值等知识点,属于基础题、
解答:解:对于不等式组的第二个不等式:x+a>0,可以解得x>-a…①
(1)当a=0时,不等式第一个不等式为0>-1,解集为R,可得原不等式组解集不是空集,符合题意;
(2)当a>0时,不等式第一个不等式的解为:x>
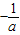 ,结合①可得交集不是空集,符合题意;
,结合①可得交集不是空集,符合题意;(3)当a<0时,不等式第一个不等式的解为:x<
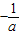 …②,
…②,i.当a≤-1时,-a≥
 ,对照①②可得不等式组的解集是空集;
,对照①②可得不等式组的解集是空集;ii.当-1<a<0时,-a<
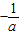 ,对照①②可得不等式组的解集是(-a,
,对照①②可得不等式组的解集是(-a,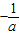 ),符合题意.
),符合题意.综上所述,当原不等式的解集不是空集时,a>-1.
故选C
点评:本题以不等式的解集非空为例,考查了含有参数不等式的解法和集合关系中参数取值等知识点,属于基础题、

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目

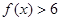 ;
; 的不等式
的不等式 的解集不是空集,求
的解集不是空集,求 得取值范围.
得取值范围.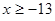 ,关于
,关于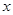 的不等式
的不等式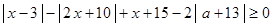 的解集不是空集,求实数
的解集不是空集,求实数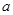 的取值范围.
的取值范围. 的解集不是空集,则实数a的取值范围为______.
的解集不是空集,则实数a的取值范围为______. 的不等式
的不等式 的解集不是空集,则
的解集不是空集,则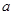 的取值范围 。
的取值范围 。