题目内容
(本小题满分14分)
已知 的周长为
的周长为 ,且
,且 ,
, 的面积为
的面积为 ,
,
(1)求边 的长;
的长;
(2)求 的值.
的值.
已知
 的周长为
的周长为 ,且
,且 ,
, 的面积为
的面积为 ,
,(1)求边
 的长;
的长;(2)求
 的值.
的值.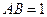
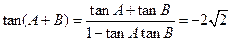
解:(新编题)
(1)因为 的周长为
的周长为 ,所以
,所以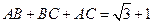 .----------1分
.----------1分
又 ,由正弦定理得
,由正弦定理得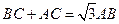 .--------------3分
.--------------3分
两式相减,得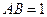 .--------------------------------------------------------------------4分
.--------------------------------------------------------------------4分
(2)由于 的面积
的面积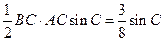 ,得
,得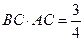 ,-----6分
,-----6分
由余弦定理得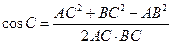 --------------------------------------------8分
--------------------------------------------8分
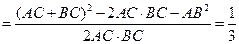 ,---------------------10分
,---------------------10分
又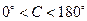 ,所以
,所以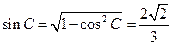 .-----------------------------12分
.-----------------------------12分
故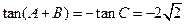 .------------------------------------14分
.------------------------------------14分
另解:由(1)得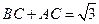 ,又
,又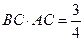 ,
,
所以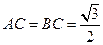 ------------------------------------------------------------------------6分
------------------------------------------------------------------------6分
在 中,作
中,作 于
于 ,则
,则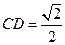 ,---------------------------------8分
,---------------------------------8分
所以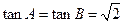 -------------------------------------------------------------------10分
-------------------------------------------------------------------10分
故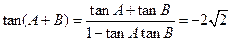 ---------------------------14分
---------------------------14分
(1)因为
 的周长为
的周长为 ,所以
,所以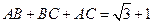 .----------1分
.----------1分又
 ,由正弦定理得
,由正弦定理得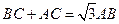 .--------------3分
.--------------3分两式相减,得
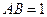 .--------------------------------------------------------------------4分
.--------------------------------------------------------------------4分(2)由于
 的面积
的面积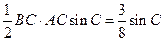 ,得
,得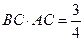 ,-----6分
,-----6分由余弦定理得
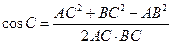 --------------------------------------------8分
--------------------------------------------8分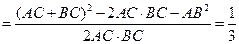 ,---------------------10分
,---------------------10分又
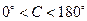 ,所以
,所以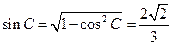 .-----------------------------12分
.-----------------------------12分故
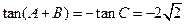 .------------------------------------14分
.------------------------------------14分另解:由(1)得
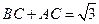 ,又
,又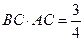 ,
,所以
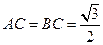 ------------------------------------------------------------------------6分
------------------------------------------------------------------------6分在
 中,作
中,作 于
于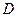 ,则
,则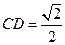 ,---------------------------------8分
,---------------------------------8分所以
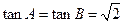 -------------------------------------------------------------------10分
-------------------------------------------------------------------10分故
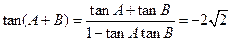 ---------------------------14分
---------------------------14分
练习册系列答案
相关题目
 中,
中,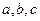 分别是角
分别是角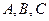 的对边,
的对边,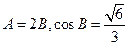 ,求
,求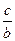 的值.
的值.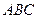 中,角
中,角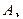
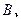
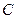 的对边分别为
的对边分别为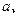
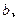
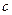 ,
, . (1)求角
. (1)求角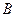 的大小.
的大小.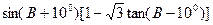 的值.
的值.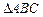 的外接圆半径为
的外接圆半径为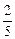 ,且
,且 ,求
,求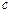 边的长.
边的长.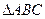 中,角
中,角 的对边分别为
的对边分别为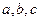 ,且
,且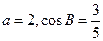 .
.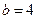 ,求
,求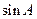 ;
;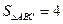 ,求
,求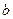 的值.
的值.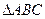 中,若
中,若 ,
,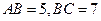 ,则
,则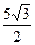
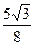
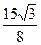
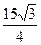
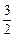 ≤a<3
≤a<3 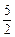
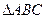 中,若
中,若
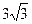 ,则
,则