题目内容
已知0
，且点（1，cosθ）到直线xsinθ+ycosθ=1的距离等于
，则θ等于 ．
【答案】分析：由点到直线的距离公式求出sinθ的值，再结合θ的范围，求出θ的大小即可．
解答：解：由题意结合点到直线的距离公式可得：
=
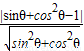=|sinθ-sin2θ|，
又0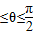
，故0≤sinθ≤1，所以|sinθ-sin2θ|=sinθ-sin2θ=
，
∴sin2θ-sinθ+
=0，解得sinθ=
，又0
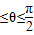，故θ=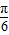
故答案为：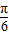
点评：本题考查点到直线的距离公式的应用和已知三角函数值求角的方法，属基础题．
解答：解：由题意结合点到直线的距离公式可得：
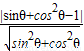==|sinθ-sin2θ|，又0
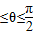，故0≤sinθ≤1，所以|sinθ-sin2θ|=sinθ-sin2θ=，∴sin2θ-sinθ+
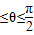=0，解得sinθ=，又0，故θ=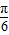故答案为：
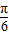
点评：本题考查点到直线的距离公式的应用和已知三角函数值求角的方法，属基础题．
练习册系列答案
黄冈创优卷系列答案
相关题目
D.
在点p(1,4)处的切线与直线l平行且距离为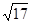
,则直线l的方程为（ ）
相切，则动圆圆心的轨迹方程为 （ ）
B．
D．
的左、右两焦点分别为F1，F2，P是椭圆C上的一点，且在x轴的上方，H是PF1上一点，若
，
（其中O为坐标原点）， 
，求直线l的方程。 
=1上的一点.已知
=0，且
.
=0，求双曲线C的方程.