题目内容
(本题满分12分)已知函数![]() ,g (x) =-6x + ln x3(a≠0).
,g (x) =-6x + ln x3(a≠0).
(Ⅰ)若函数h (x) = f (x)-g (x) 有两个极值点,求实数a的取值范围;
(Ⅱ)是否存在实数a>0,使得方程g (x) = x f ′(x)-3(2a + 1)x 无实数解?若存在,求出a的取值范围?若不存在,请说明理由.
解 (Ⅰ)∵ h (x) = f (x)-g (x) =![]() + 6x-3 ln x(x>0),
+ 6x-3 ln x(x>0),
∴ ![]() . …………………… 2分
. …………………… 2分
∵ 函数h (x) 有两个极值点,∴ 方程![]() ,
,
即ax2 + 2x-1 = 0应有两个不同的正数根,于是 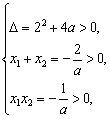
Þ -1<a<0. …………………… 6分
(Ⅱ)方程 g (x) = x f ′(x)-3(2a + 1)x 即为 -6x + 3 ln x = 3ax2-3(2a + 1)x,
等价于方程 ax2 +(1-2a)x-ln x = 0.
设 H(x)= ax2 +(1-2a)x-ln x,转化为关于函数H(x)在区间(0,+∞)内的零点问题(即函数H(x)图象与x轴有无交点的问题). …………………… 8分
∵ H ′(x) = 2ax +(1-2a)-![]() ,
,
且a>0,x>0,则当x∈(0,1)时,H ′(x)<0,H(x)是减函数;
当x∈(1,+∞)时,H ′(x)>0,H(x)是增函数. …………………… 10分
因为 x ® 0(或者x ®+∞)时,H(x)® +∞,
∴ 要使H(x)图象与x轴有无交点,只需
H(x)min = H(1)= a +(1-2a)= 1-a>0,结合a>0得 0<a<1,为所求.
…………………… 12分

 的三个内角
的三个内角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 .
. ,且
,且 .(1)求
.(1)求 .求
.求 .
. ,
, 的等比中项。
的等比中项。 是等差数列;(2)若
是等差数列;(2)若 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。 :
: 的长轴长是短轴长的
的长轴长是短轴长的 倍,
倍, ,
, 是它的左,右焦点.
是它的左,右焦点. ,且
,且 ,
, ,求
,求 作以
作以 (
( 是切点),且使
是切点),且使 ,求动点
,求动点 的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量
的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量 与
与 是共线向量
是共线向量 分别是左右焦点,求
分别是左右焦点,求 的取值范围
的取值范围