Question

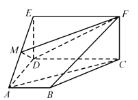
【题目】如图,四棱锥P﹣ABCD的底面ABCD是平行四边形,∠BCD=135°,PA⊥平面ABCD,AB=AC=PA=2,E,F,M分别为线段BC,AD,PD的中点.

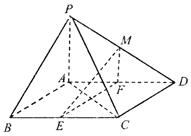
（1）求证:直线EF⊥平面PAC;

（2）求平面MEF与平面PBC所成二面角的正弦值.

Answer 1

【答案】（1）答案见解析.（2）

【解析】

（1）推导出AB⊥AC，EF∥AB，从而EF⊥AC，由PA⊥底面ABCD，得PA⊥EF，由此能证明EF⊥平面PAC.

（2）以AB，AC，AP分别为x，y，z轴，建立空间直角坐标系，求体积出平面PBC的一个法向量，再利用向量法求二面角的正弦值.

（1）证明：在平行四边形ABCD中，

∵AB=AC，∠BCD=135°，∴AB⊥AC，

∵E，F，M分别为线段BC，AD，PD的中点.∴EF∥AB，

∴EF⊥AC，

∵PA⊥底面ABCD，EF底面ABCD，∴PA⊥EF，

∵PA∩AC=A，∴EF⊥平面PAC.

（2）∵PA⊥底面ABCD，AB⊥AC，∴AP，AB，AC两两垂直，

如图所示：

以AB，AC，AP分别为x，y，z轴，建立空间直角坐标系，

则A(0，0，0)，B(2，0，0)，C(0，2，0)，P(0，0，2)，D(﹣2，2，0)，E(1，1，0)，

=(﹣2，2，0)， =(2，0，﹣2)，

设平面PBC的法向量=(x，y，z)，

则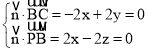，取x=1，得=(1，1，1)，

M是PD的中点，由（1）知，AC⊥平面MEF，且=(0，2，0)，

∴|=，

∴平面MEF与平面PBC所成二面角的正弦值为.