题目内容
对于数列{an},定义{△an}为数列{an}的一阶差分数列,其中△an=an+1-an,n∈N*;对k≥2,k∈N*,定义{△kan}为{an}的k阶差分数列,其中△kan=△k-1an+1-△k-1an.
(1)若数列{an}的通项公式为an=n2-6n,分别求出其一阶差分数列{△an}、二阶差分数列{△2an}的通项公式;
(2)若数列{an}首项a1=1,且满足△2an-△an+1+an=-2n,求出数列{an}的通项公式an及前n项和Sn.
(1)若数列{an}的通项公式为an=n2-6n,分别求出其一阶差分数列{△an}、二阶差分数列{△2an}的通项公式;
(2)若数列{an}首项a1=1,且满足△2an-△an+1+an=-2n,求出数列{an}的通项公式an及前n项和Sn.
分析:(1)利用一阶差分数列与k阶差分数列的概念即可求得通项公式为an=n2-6n的数列{an}的一阶差分数列{△an}、二阶差分数列{△2an}的通项公式;
(2)由△2an-△an+1+an=-2n,可求得
=
+
,继而可求得an=n•2n-1,利用错位相减法即可求得其前n项和Sn.
(2)由△2an-△an+1+an=-2n,可求得
| an+1 |
| 2n+1 |
| an |
| 2n |
| 1 |
| 2 |
解答:解:(1)△an=an+1-an=[(n+1)2-6(n+1)]-(n2-6n)=2n-5…3分
△2an=△an+1-△an=[2(n+1)-5]-(2n-5)=2…2分
(2)由△2an-△an+1+an=-2n,
则△an+1-△an-△an+1+an=-2n
即△an-an=2n,
∴an+1-an=an+2n,即an+1=2an+2n…2分
∴
=
+
,
则{
}为公差是
的等差数列…2分
又
=
,
∴
=
+
(n-1)=
n(n∈N*),
∴an=n•2n-1…2分
∴Sn=1•20+2•21+3•22+4•23+…+(n-1)•2n-2+n•2n-1…①
2Sn=1•21+2•22+3•23+…+(n-1)•2n-1+n•2n…②
①-②得:
-Sn=1+21+22+…+2n-1-n•2n=
-n•2n=2n-1-n•2n,
∴Sn=(n-1)2n+1(n∈N*)…2分
△2an=△an+1-△an=[2(n+1)-5]-(2n-5)=2…2分
(2)由△2an-△an+1+an=-2n,
则△an+1-△an-△an+1+an=-2n
即△an-an=2n,
∴an+1-an=an+2n,即an+1=2an+2n…2分
∴
| an+1 |
| 2n+1 |
| an |
| 2n |
| 1 |
| 2 |
则{
| an |
| 2n |
| 1 |
| 2 |
又
| a1 |
| 2 |
| 1 |
| 2 |
∴
| an |
| 2n |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴an=n•2n-1…2分
∴Sn=1•20+2•21+3•22+4•23+…+(n-1)•2n-2+n•2n-1…①
2Sn=1•21+2•22+3•23+…+(n-1)•2n-1+n•2n…②
①-②得:
-Sn=1+21+22+…+2n-1-n•2n=
| 1-2n |
| 1-2 |
∴Sn=(n-1)2n+1(n∈N*)…2分
点评:本题考查数列的求和,着重考查等差数列的性质与判定,考查错位相减法求和,考查逻辑推理与抽象思维能力,属于难题.

练习册系列答案
相关题目
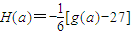 ,数列{an}满足an+1=H(an)(n∈N*),且a1∈(0,1),试判断an+1与an的大小,并证明之.
,数列{an}满足an+1=H(an)(n∈N*),且a1∈(0,1),试判断an+1与an的大小,并证明之.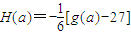 ,数列{an}满足an+1=H(an)(n∈N*),且a1∈(0,1),试判断an+1与an的大小,并证明之.
,数列{an}满足an+1=H(an)(n∈N*),且a1∈(0,1),试判断an+1与an的大小,并证明之.