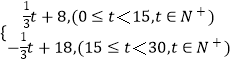题目内容
【题目】已知y=f(x)是定义在R上的奇函数,当x>0时,f(x)=x2﹣2x.
(1)画出f(x)的简图,并求f(x)的解析式; 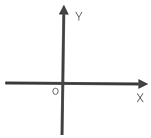
(2)利用图象讨论方程f(x)=k的根的情况.(只需写出结果,不要解答过程).
【答案】
(1)解:由题意:函数y=f(x)是定义在R上的奇函数,
∴f(﹣x)=﹣f(x),当x=0时,有f(0)=0.
当x>0时,f(x)=x2﹣2x,
当x<0时,则﹣x>0,
那么:f(﹣x)=x2+2x,
∵f(﹣x)=﹣f(x),
∴f(x)=﹣x2﹣2x
f(x)是定义在R上的解析式为f(x)= 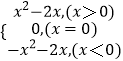
(简图(如右图) 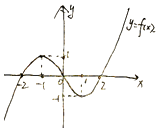
(2)解:根据图象:当k=±1时,有2个实数根,
当﹣1<k<1时,有3个实数根,
当k>1或k<﹣1时,方程有1个实根
【解析】(1)根据y=f(x)是定义在R上的奇函数,当x>0时,f(x)=x2﹣2x.求出f(x)的解析式.作图.(2)根据函数图象与函数y=k的交点,即可判断根的情况.
【考点精析】利用函数奇偶性的性质对题目进行判断即可得到答案,需要熟知在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目