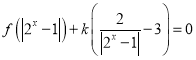题目内容
【题目】已知函数
在区间
上的最大值为3，最小值为-17，求
的值
【答案】k=﹣1，B=﹣17或k=1，B=3
【解析】
试题分析：由题设知k≠0且f'（x）=3kx（x-2），0＜x＜2时，x（x-2）＜0；x＜0或x＞2时，x（x-2）＞0；x=0和x=2时，f'（x）=0．由题设知-2≤x≤2，f（-2）=-20k+B，f（0）=B，f（2）=-4k+B．由此能够求出k、B的值
试题解析：由题设知k≠0且f'（x）=3kx（x﹣2），0＜x＜2时，x（x﹣2）＜0；
x＜0或x＞2时，x（x﹣2）＞0； x=0和x=2时，f'（x）=0．
由题设知﹣2≤x≤2，f（﹣2）=﹣20k+B，f（0）=B，f（2）=﹣4k+B
①k＜0时，﹣2＜x＜0时，f'（x）＜0；0＜x＜2时，f'（x）＞0，
∴f（x）在[﹣2，0）上递减，在（0，2）上递增，
x=0为最小值点；∵f（﹣2）＞f（2）∴f（x）的最大值是f（﹣2）
即
，解得k=-1，B=-17
②k＞0时，
，解得k=1，B=3
综上，k=﹣1，B=﹣17或k=1，B=3
练习册系列答案
阳光同学一线名师全优好卷系列答案
相关题目
