��Ŀ����
��ƽ��ֱ����������һ����P1��x1��y1����P2��x2��y2������Pn��xn��yn��������һ��������n����Pn�ں���y=3x+
| 13 |
| 4 |
| 5 |
| 2 |
�������Pn�����ꣻ
��������������C1��C2��C3����Cn�����е�ÿһ���ĶԳ��ᶼ��ֱ��x�ᣬ������Cn�Ķ���ΪPn���ҹ���Dn��0��n2+1��������������Cn�����ڵ�Dn��ֱ�ߵ�б��ΪKn����
| 1 |
| k1k2 |
| 1 |
| k2k3 |
| 1 |
| knkn+1 |
��������I�����ݵȲ����е�ͨ�ʽ�����xn����������ֱ�߷������yn�����P������ɵã�
��II�������Cn�ķ��̣���D��������a�������Ժ����������������ߵ�б�ʣ���kn�ı���ʽ��������������
+
+��+
��II�������Cn�ķ��̣���D��������a�������Ժ����������������ߵ�б�ʣ���kn�ı���ʽ��������������
| 1 |
| k1k2 |
| 1 |
| k2k3 |
| 1 |
| kn-1kn |
����⣺��1����xn=-
+(n-1)��(-1)=-n-
��
��yn=3xn+
=-3n-
��
��Pn(-n-
��-3n-
)��
��2����Cn�ĶԳ��ᴹֱ��x�ᣬ�Ҷ���ΪPn��
����Cn�ķ���Ϊ y=a(x+
)2-
��
��Dn��0��n2+1��������ʽ����a=1��
��Cn�ķ���Ϊy=x2+��2n+3��x+n2+1��
��kn=y'|x=0=2n+3��
��
=
=
[
-
]��
��
+
+
=
[(
-
)+(
-
)++(
-
)]
=
(
-
)=
-
��
| 5 |
| 2 |
| 3 |
| 2 |
��yn=3xn+
| 13 |
| 4 |
| 5 |
| 4 |
��Pn(-n-
| 3 |
| 2 |
| 5 |
| 4 |
��2����Cn�ĶԳ��ᴹֱ��x�ᣬ�Ҷ���ΪPn��
����Cn�ķ���Ϊ y=a(x+
| 2n+3 |
| 2 |
| 12n+5 |
| 4 |
��Dn��0��n2+1��������ʽ����a=1��
��Cn�ķ���Ϊy=x2+��2n+3��x+n2+1��
��kn=y'|x=0=2n+3��
��
| 1 |
| kn-1kn |
| 1 |
| (2n+1)(2n+3) |
| 1 |
| 2 |
| 1 |
| (2n+1) |
| 1 |
| (2n+3) |
��
| 1 |
| k1k2 |
| 1 |
| k2k3 |
| 1 |
| kn-1kn |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 7 |
| 1 |
| 9 |
| 1 |
| 2n+1 |
| 1 |
| 2n+3 |
=
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 2n+3 |
| 1 |
| 10 |
| 1 |
| 4n+6 |
�����������е�ǰn��͵����⣬һ����������е�ͨ�ʽ������ͨ�ʽ���ص㣬ѡ����ʵ���ͷ�������������ͷ����У���ʽ����������ӷ�����λ����������������������鷨��

��ϰ��ϵ�д�
�����Ŀ
 ��ͼ���ϣ���Pn�ĺ����깹����-
��ͼ���ϣ���Pn�ĺ����깹����- Ϊ���-1Ϊ����ĵȲ�����{xn}��
Ϊ���-1Ϊ����ĵȲ�����{xn}��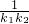 +
+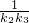 +��+
+��+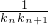 ��ֵ��
��ֵ�� ��ͼ���ϣ���Pn�ĺ����깹����-
��ͼ���ϣ���Pn�ĺ����깹����- Ϊ���-1Ϊ����ĵȲ�����{xn}��
Ϊ���-1Ϊ����ĵȲ�����{xn}�� +
+ +��+
+��+ ��ֵ��
��ֵ��