题目内容
在平面直角坐标上有一点列P1(x1,y1),P2(x2,y2)…,Pn(xn,yn)…,对一切正整数n,点Pn在函数y=3x+
 的图象上,且Pn的横坐标构成以-
的图象上,且Pn的横坐标构成以- 为首项,-1为公差的等差数列{xn}.
为首项,-1为公差的等差数列{xn}.(Ⅰ)求点Pn的坐标;
(Ⅱ)设抛物线列C1,C2,C3,…Cn,…中的每一条的对称轴都垂直于x轴,抛物线Cn的顶点为Pn,且过点Dn(0,n2+1),记与抛物线Cn相切于点Dn的直线的斜率为Kn,求
 +
+ +…+
+…+ 的值.
的值.
【答案】分析:(I)根据等差数列的通项公式可求得xn,进而代入直线方程求得yn,则点P的坐标可得.
(II)先设出Cn的方程,把D点代入求得a,进而对函数进行求得求得切线的斜率,即kn的表达式,进而用裂项法求得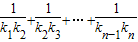
解答:解:(1)∵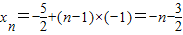 ,
,
∴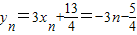 .
.
∴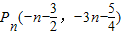 .
.
(2)∵Cn的对称轴垂直于x轴,且顶点为Pn,
∴设Cn的方程为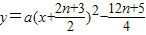 .
.
把Dn(0,n2+1)代入上式,得a=1,
∴Cn的方程为y=x2+(2n+3)x+n2+1.
∵kn=y'|x=0=2n+3,
∴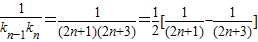 ,
,
∴ =
=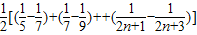
= .
.
点评:求数列的前n项和的问题,一般先求出数列的通项公式,根据通项公式的特点,选择合适的求和方法.常见的求和方法有:公式法、倒序相加法、错位相减法、裂项相消法、分组法.
(II)先设出Cn的方程,把D点代入求得a,进而对函数进行求得求得切线的斜率,即kn的表达式,进而用裂项法求得
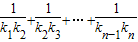
解答:解:(1)∵
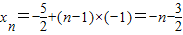 ,
,∴
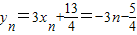 .
.∴
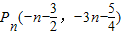 .
.(2)∵Cn的对称轴垂直于x轴,且顶点为Pn,
∴设Cn的方程为
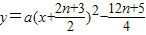 .
.把Dn(0,n2+1)代入上式,得a=1,
∴Cn的方程为y=x2+(2n+3)x+n2+1.
∵kn=y'|x=0=2n+3,
∴
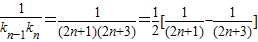 ,
,∴
 =
=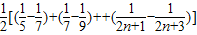
=
 .
.点评:求数列的前n项和的问题,一般先求出数列的通项公式,根据通项公式的特点,选择合适的求和方法.常见的求和方法有:公式法、倒序相加法、错位相减法、裂项相消法、分组法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的图象上,且Pn的横坐标构成以-
的图象上,且Pn的横坐标构成以- 为首项,-1为公差的等差数列{xn}.
为首项,-1为公差的等差数列{xn}.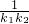 +
+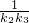 +…+
+…+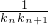 的值.
的值.