题目内容
13.已知tanα=3,求:(1)$\frac{sin(α-3π)-2cos(\frac{2015π}{2}+α)}{-sin(-α)+cos(π+α)}$.
(2)2sin2α+sinαcosα
分析 (1)由诱导公式、商的关系化简已知的齐次分式,把tanα=3代入求值;
(2)由平方关系、商的关系化简已知的式子,把tanα=3代入求值.
解答 解:(1)因为tanα=3,
所以式子=$\frac{sin(α-π-2π)-2cos(1006π+\frac{3π}{2}+α)}{sinα-cosα}$
=$\frac{sin(α-π)-2cos(\frac{3π}{2}+α)}{sinα-cosα}$=$\frac{-sin(π-α)+2cos(\frac{π}{2}+α)}{sinα-cosα}$
=$\frac{-sinα-2sinα}{sinα-cosα}$=$\frac{-3tanα}{tanα-1}$=$\frac{-3×3}{3-1}$=-$\frac{9}{2}$;
(2)因为tanα=3,
所以式子=$\frac{2si{n}^{2}α+sinαcosα}{si{n}^{2}α+co{s}^{2}α}$=$\frac{2{tan}^{2}α+tanα}{ta{n}^{2}α+1}$
=$\frac{2×9+3}{9+1}$=$\frac{21}{10}$.
点评 本题考查同角基本三角函数关系,诱导公式的灵活应用,考查化简、变形能力,属于中档题.

练习册系列答案
相关题目
18.已知函数f(x)满足f(log2x)=$\sqrt{{x}^{2}-2x+1}$,若a<b<c,且f(a)>f(c)>f(b),则( )
| A. | a<0,b<0,c<0 | B. | a<0,b≥0,c>0 | C. | 2-a<2c | D. | 2a+2c<2 |
5.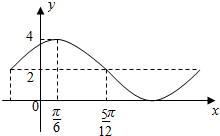 已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,||φ|<$\frac{π}{2}$,则( )
已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,||φ|<$\frac{π}{2}$,则( )
 已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,||φ|<$\frac{π}{2}$,则( )
已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,||φ|<$\frac{π}{2}$,则( )| A. | B=1 | B. | φ=$\frac{π}{6}$ | C. | ω=1 | D. | A=4 |