题目内容

8. 点在直线：上，若存在过的直线交抛物线于，两点，且，则称点为“点”，那么下列结论中正确的是

  A．直线上的所有点都是“点”    B．直线上仅有有限个点是“点”

  C．直线上的所有点都不是“点”  D．直线上有无穷多个点（点不是所有的点）是“点”

A


解析:

本题采作数形结合法易于求解，如图，

设，，

∵，∴，

∵点在抛物线上，

∴

整理得关于的方程            （*）

∵恒成立，

∴方程（*）恒有实数解，∴应选A.

练习册系列答案
相关题目
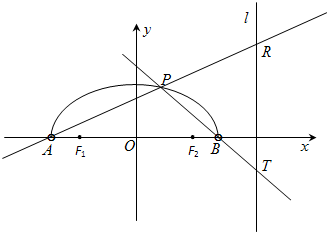精英家教网如图，在x轴上方有一段曲线弧Γ，其端点A、B在x轴上（但不属于Γ），对Γ上任一点P及点F1（-1，0），F2（1，0），满足：|PF1|+|PF2|=2
2
．直线AP，BP分别交直线l：x=a (a＞
2
)于R，T两点．
（1）求曲线弧Γ的方程；
（2）求|RT|的最小值（用a表示）；
（3）曲线Γ上是否存点P，使△PRT为正三角形？若存在，求a的取值范围；若不存在，说明理由．
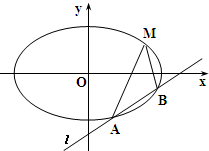精英家教网如图，已知焦点在x轴上的椭圆
x2
20
+
y2
b2
=1(b＞0)经过点M（4，1），直线l：y=x+m交椭圆于A，B两不同的点．
（1）求该椭圆的标准方程；
（2）求实数m的取值范围；
（3）是否存在实数m，使△ABM为直角三角形，若存在，求出m的值，若不存，请说明理由．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0），⊙O：x2+y2=b2，点A、F分别是椭圆C的左顶点和左焦点，点P是⊙O上的动点．
（1）若P（-1，
3
），PA是⊙O的切线，求椭圆C的方程；
（2）若
PA
PF
是一个常数，求椭圆C的离心率；
（3）当b=1时，过原点且斜率为k的直线交椭圆C于D、E两点，其中点D在第一象限，它在x轴上的射影为点G，直线EG交椭圆C于另一点H，是否存实数a，使得对任意的k＞0，都有DE⊥DH？若存在，求出a的值，若不存在，请说明理由．
已知中心在原点，焦点在x轴上的椭圆C的离心率为
1
2
，且经过点M(1，
3
2
)．
（Ⅰ）求椭圆C的方程；
（Ⅱ）是否存过点P（2，1）的直线l1与椭圆C相交于不同的两点A，B，满足
PA
•
PB
=
PM
2？若存在，求出直线l1的方程；若不存在，请说明理由．
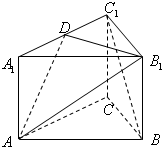精英家教网如图，正三棱柱ABC-A1B1C1的底面边长为a，侧棱长为
2
2
a，点D在棱A1C1上．
（1）若A1D=DC1，求证：直线BC1∥平面AB1D；
（2）是否存点D，使平面AB1D⊥平面ABB1A1，若存在，请确定点D的位置，若不存在，请说明理由；
（3）请指出点D的位置，使二面角A1-AB1-D平面角的正切值的大小为2，并证明你的结论．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网