题目内容
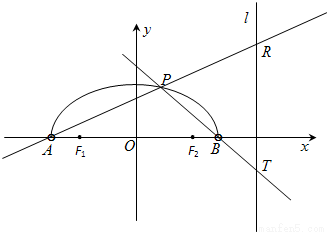
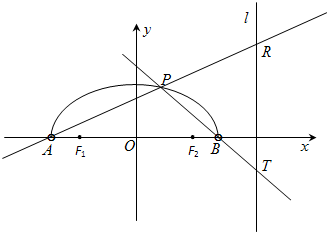 如图,在x轴上方有一段曲线弧Γ,其端点A、B在x轴上(但不属于Γ),对Γ上任一点P及点F1(-1,0),F2(1,0),满足:|PF1|+|PF2|=2
如图,在x轴上方有一段曲线弧Γ,其端点A、B在x轴上(但不属于Γ),对Γ上任一点P及点F1(-1,0),F2(1,0),满足:|PF1|+|PF2|=2| 2 |
| 2 |
(1)求曲线弧Γ的方程;
(2)求|RT|的最小值(用a表示);
(3)曲线Γ上是否存点P,使△PRT为正三角形?若存在,求a的取值范围;若不存在,说明理由.
分析:(1)由椭圆的定义和简单性质求得 Γ的方程.
(2) 设出P,R,T的坐标,由A,P,R三点共线,得
=
①,由B,P,T三点共线得:
=
②,变形得即y1y2=
(2-a2).利用基本不等式求出|RT|的最小值.
(3)设P(x0,y0),线AP,BP的斜率存在,分别设为k1、k2 ,由正三角形的性质得k1•k2=
=-
,
而由椭圆的方程知
=-
,矛盾,故不存在点P,使△PRT为正三角形.
(2) 设出P,R,T的坐标,由A,P,R三点共线,得
| y1 | ||
a+
|
| n | ||
m+
|
| y2 | ||
a-
|
| n | ||
m-
|
| 1 |
| 2 |
(3)设P(x0,y0),线AP,BP的斜率存在,分别设为k1、k2 ,由正三角形的性质得k1•k2=
| ||
|
| 1 |
| 3 |
而由椭圆的方程知
| ||
|
| 1 |
| 2 |
解答:解:(1)由椭圆的定义,曲线Γ是以F1(-1,0),F2(1,0)为焦点的半椭圆,c=1 , a=
, b2=a2-c2=1,∴Γ的方程为
+y2=1 (y>0).
(2)解:设P(m,n),R(a,y1),T(a,y2),则由A,P,R三点共线,得
=
①,
同理,由B,P,T三点共线得:
=
②,由①×②得:
=
.
由
+n2=1?n2=1-
,代入上式,
=
=-
.
即y1y2=
(2-a2).
|RT|=|y1-y2|=
≥
=
,
当且仅当|y1|=|y2|,即y1=-y2时,取等号.
即|RT|的最小值是
.
(3)设P(x0,y0),依题设,直线l∥y轴,若△PRT为正三角形,则必有∠PAB=180°-∠PBx=30°,
从而直线AP,BP的斜率存在,分别设为k1、k2,由 k1=
=
;k2=
=-
,
于是有k1•k2=
=-
,而由椭圆的方程知
=-
,矛盾.
∴不存在点P,使△PRT为正三角形.(14分)
| 2 |
| x2 |
| 2 |
(2)解:设P(m,n),R(a,y1),T(a,y2),则由A,P,R三点共线,得
| y1 | ||
a+
|
| n | ||
m+
|
同理,由B,P,T三点共线得:
| y2 | ||
a-
|
| n | ||
m-
|
| y1y2 |
| a2-2 |
| n2 |
| m2-2 |
由
| m2 |
| 2 |
| m2 |
| 2 |
| y1y2 |
| a2-2 |
1-
| ||
| m2-2 |
| 1 |
| 2 |
即y1y2=
| 1 |
| 2 |
|RT|=|y1-y2|=
|
| 2|y1y2|-2y1y2 |
| 2(a2-2) |
当且仅当|y1|=|y2|,即y1=-y2时,取等号.
即|RT|的最小值是
| 2(a2-2) |
(3)设P(x0,y0),依题设,直线l∥y轴,若△PRT为正三角形,则必有∠PAB=180°-∠PBx=30°,
从而直线AP,BP的斜率存在,分别设为k1、k2,由 k1=
| y0 | ||
x0+
|
| ||
| 3 |
| y0 | ||
x0-
|
| ||
| 3 |
于是有k1•k2=
| ||
|
| 1 |
| 3 |
| ||
|
| 1 |
| 2 |
∴不存在点P,使△PRT为正三角形.(14分)
点评:本题考查椭圆的定义、椭圆的标准方程,以及椭圆的简单性质的应用,正确进行式子的运算是本题的难点.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
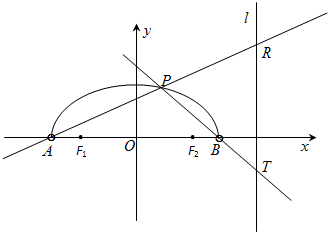 如图,在x轴上方有一段曲线弧Γ,其端点A、B在x轴上(但不属于Γ),对Γ上任一点P及点F1(-1,0),F2(1,0),满足:
如图,在x轴上方有一段曲线弧Γ,其端点A、B在x轴上(但不属于Γ),对Γ上任一点P及点F1(-1,0),F2(1,0),满足: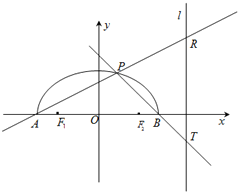 如图,在x轴上方有一段曲线弧C,其端点A、B在x轴上(但不属于C),对C上任一点P及点F1(-1,0),F2(1,0),满足:
如图,在x轴上方有一段曲线弧C,其端点A、B在x轴上(但不属于C),对C上任一点P及点F1(-1,0),F2(1,0),满足: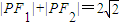 .直线AP,BP分别交直线
.直线AP,BP分别交直线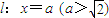 于R,T两点.
于R,T两点.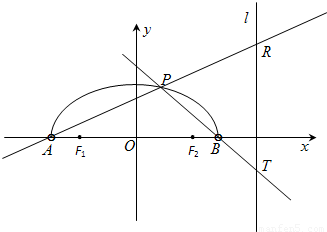
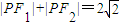 .直线AP,BP分别交直线
.直线AP,BP分别交直线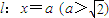 于R,T两点.
于R,T两点.