题目内容
解下列不等式:
(1)x2-x-6<0;(2)-x2+3x+10<0;(3)
≥0.
(1)x2-x-6<0;(2)-x2+3x+10<0;(3)
| x(x+1)(x-2) | (x+2)(x-1) |
分析:(1)把不等式左边分解因式,讨论x+3与x-2异号即可得到解集;
(2)先把不等式两边除以-1变形后,左边分解因式,讨论x-5与x+2同号即可得到解集;
(3)先根据分母不为0,把不等式转化为x(x+1)(x-2)(x+2)(x-1)大于等于0,利用数轴即可求出解集.
(2)先把不等式两边除以-1变形后,左边分解因式,讨论x-5与x+2同号即可得到解集;
(3)先根据分母不为0,把不等式转化为x(x+1)(x-2)(x+2)(x-1)大于等于0,利用数轴即可求出解集.
解答:解:(1)原不等式可化为为(x-3)(x+2)<0,即
或
解得-2<x<3;
(2)两边除以-1得x2-3x-10>0,因式分解得(x-5)(x+2)>0,即
或
解得x>5或x<-2;
(3)原不等式可化为
如图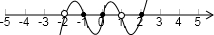
当x取数轴上边的区间即-2<x≤-1,0≤x<1,x≥2时,x(x+1)(x-2)(x+2)(x-1)中负因式的个数为偶数个即乘积大于0且x≠-2,x≠1
则原不等式的解集为:-2<x≤-1或0≤x<1或x≥2.
|
|
(2)两边除以-1得x2-3x-10>0,因式分解得(x-5)(x+2)>0,即
|
|
(3)原不等式可化为
|
如图
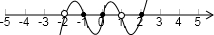
当x取数轴上边的区间即-2<x≤-1,0≤x<1,x≥2时,x(x+1)(x-2)(x+2)(x-1)中负因式的个数为偶数个即乘积大于0且x≠-2,x≠1
则原不等式的解集为:-2<x≤-1或0≤x<1或x≥2.
点评:本题考查一元二次不等式的解法,以及利用数轴求其他不等式的解集,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目