题目内容
已知等差数列{an}满足a2+a4=4,a3+a5=10,则它的前10项的和S10=
- A.138
- B.135
- C.95
- D.23
C
分析:本题考查的知识点是等差数列的性质,及等差数列前n项和,根据a2+a4=4,a3+a5=10我们构造关于基本量(首项及公差)的方程组,解方程组求出基本量(首项及公差),进而代入前n项和公式,即可求解.
解答:∵(a3+a5)-(a2+a4)=2d=6,
∴d=3,a1=-4,
∴S10=10a1+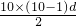 =95.
=95.
故选C
点评:在求一个数列的通项公式或前n项和时,如果可以证明这个数列为等差数列,或等比数列,则可以求出其基本项(首项与公差或公比)进而根据等差或等比数列的通项公式,写出该数列的通项公式,如果未知这个数列的类型,则可以判断它是否与某个等差或等比数列有关,间接求其通项公式.
分析:本题考查的知识点是等差数列的性质,及等差数列前n项和,根据a2+a4=4,a3+a5=10我们构造关于基本量(首项及公差)的方程组,解方程组求出基本量(首项及公差),进而代入前n项和公式,即可求解.
解答:∵(a3+a5)-(a2+a4)=2d=6,
∴d=3,a1=-4,
∴S10=10a1+
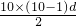 =95.
=95.故选C
点评:在求一个数列的通项公式或前n项和时,如果可以证明这个数列为等差数列,或等比数列,则可以求出其基本项(首项与公差或公比)进而根据等差或等比数列的通项公式,写出该数列的通项公式,如果未知这个数列的类型,则可以判断它是否与某个等差或等比数列有关,间接求其通项公式.

练习册系列答案
相关题目
 已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.
已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.