题目内容
已知函数f(x)=
,分别给出下面几个结论,其中正确结论的序号有
①f(x)是奇函数;
②函数f(x)的值域为R;
③函数g(x)=f(x)+x有三个零点;
④当x1,x2∈(-∞,-1),且x1≠x2,则
>f(
)恒成立.
| x |
| 1-|x| |
①②③④
①②③④
.①f(x)是奇函数;
②函数f(x)的值域为R;
③函数g(x)=f(x)+x有三个零点;
④当x1,x2∈(-∞,-1),且x1≠x2,则
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
分析:①利用奇函数的定义进行验证f(-x)=
=-f(x);②当x>0时,f(x)=
=-1+
,可求其值域,由①知当x<0时,可求f(x)值域,x=0时,f(x)=0,从而即可判断;③由图象知f(x)的图象与y=-x有三个交点,故可判断;④根据
>f(
)体现在图象是表示图象是下凹的,结合函数的图象进行判断即可.
| -x |
| 1-|-x| |
| x |
| 1-x |
| 1 |
| 1-x |
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
解答: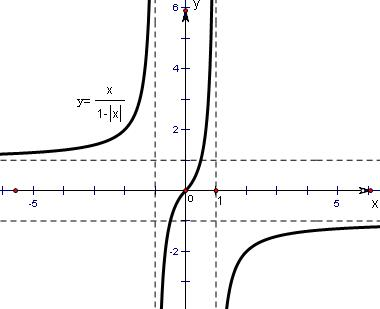 解:①f(-x)=
解:①f(-x)=
=-f(x)∴正确;
②当x>0时,f(x)=
=-1+
∈(0,+∞)∪(-∞,-1)
由①知当x<0时,f(x)=
∈(1,+∞)∪(-∞,0)
x=0时,f(x)=0
∴函数 f (x) 的值域为R,故正确;
③由图象知f(x)的图象与y=-x有三个交点,原点及第二、四象限各一个,
∴函数g(x)=f(x)+x有三个零点,故正确.
④
>f(
)体现在图象是表示图象是下凹的,结合函数在(-∞,-1)上的图象,其是下凹的,故④正确.
故答案为:①②③④.
 解:①f(-x)=
解:①f(-x)=| -x |
| 1-|-x| |
②当x>0时,f(x)=
| x |
| 1-x |
| 1 |
| 1-x |
由①知当x<0时,f(x)=
| x |
| x+1 |
x=0时,f(x)=0
∴函数 f (x) 的值域为R,故正确;
③由图象知f(x)的图象与y=-x有三个交点,原点及第二、四象限各一个,
∴函数g(x)=f(x)+x有三个零点,故正确.
④
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
故答案为:①②③④.
点评:本题综合考查函数的图象、性质及函数的零点,注意数形结合思想和函数与方程思想的应用.属中档题

练习册系列答案
相关题目