题目内容
计算求值:
(1)已知10α=2 -
,10β=32
,求10 2α-
β的值
(2)计算:lg500+lg
-
lg64+50(lg2+lg5)2.
(1)已知10α=2 -
| 1 |
| 2 |
| 1 |
| 3 |
| 3 |
| 4 |
(2)计算:lg500+lg
| 8 |
| 5 |
| 1 |
| 2 |
分析:(1)直接利用指数式的运算性质化简求值;
(2)直接利用对数式的运算性质化简求值.
(2)直接利用对数式的运算性质化简求值.
解答:解:(1)由10α=2 -
,10β=32
,
则10 2α-
β=
=
=
=
=
=2-
;
(2)lg500+lg
-
lg64+50(lg2+lg5)2
=lg5+2+lg8-lg5-
lg26+50
=2+3lg3-3lg2+50=52.
| 1 |
| 2 |
| 1 |
| 3 |
则10 2α-
| 3 |
| 4 |
| 102α | ||
10
|
| (10α)2 | ||
(10β)
|
(2-
| ||||
(32
|
=
| 2-1 | ||
32
|
| 2-1 | ||
2
|
| 9 |
| 4 |
(2)lg500+lg
| 8 |
| 5 |
| 1 |
| 2 |
=lg5+2+lg8-lg5-
| 1 |
| 2 |
=2+3lg3-3lg2+50=52.
点评:本题考查了有理指数幂的化简与求值,考查了指数式与对数式的互化,关键是lg2+lg5=1的运用,是基础的计算题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
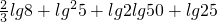 的值;
的值;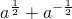 的值.
的值. 的值;
的值;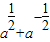 的值.
的值.