题目内容
计算:(1)已知a-a-1=1,求
的值.
(2)(lg2)3+3lg2•lg5+(lg5)3的值.
| a2+a-2-3 | a4-a-4 |
(2)(lg2)3+3lg2•lg5+(lg5)3的值.
分析:(1)根据已知a-a-1=1,把a+a-2配成完全平方差的形式,可知原式的分子为零,因此可以求得结果;
(2)对于(lg2)3+(lg5)3利用立方和公式进行因式分解,再根据lg2+lg5=1,即可求得结果.
(2)对于(lg2)3+(lg5)3利用立方和公式进行因式分解,再根据lg2+lg5=1,即可求得结果.
解答:解:(1)a+a-2=(a-a-1)2+2=3
∴原式=0
(2)原式=(lg2+lg5)[(lg2)2-lg2lg5+(lg5)2]+3lg2•lg5
=(lg2)2+2lg2•lg5+(lg5)2
=(lg2+lg5)2
=1
∴原式=0
(2)原式=(lg2+lg5)[(lg2)2-lg2lg5+(lg5)2]+3lg2•lg5
=(lg2)2+2lg2•lg5+(lg5)2
=(lg2+lg5)2
=1
点评:本题考查指数幂的化简求值和对数的运算性质,特别对于给值求值问题,注意整体代换的解题策略,属基础题.

练习册系列答案
相关题目
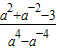 的值.
的值.