题目内容
（附加题）已知 a、b、c、d都是正数，求证1＜
+
+
+
＜2．
| a |
| a+b+d |
| b |
| b+c+a |
| c |
| c+d+b |
| d |
| d+a+c |
分析：由不等式性质可得
+
+
+
＞
+
+
+
，且
+
+
+
＜
+
+
+
，由此证得不等式成立．
| a |
| a+b+d |
| b |
| b+c+a |
| c |
| c+d+b |
| d |
| d+a+c |
| a |
| a+b+c+d |
| b |
| a+b+c+d |
| c |
| a+b+c+d |
| d |
| a+b+c+d |
| a |
| a+b+d |
| b |
| b+c+a |
| c |
| c+d+b |
| d |
| d+a+c |
| a+c |
| a+b+c+d |
| b+d |
| a+b+c+d |
| c+a |
| a+b+c+d |
| d+b |
| a+b+c+d |
解答：证明：∵a、b、c、d都是正数，
∴
+
+
+
＞
+
+
+
=1．
+
+
+
＜
+
+
+
=2．
综上可得，1＜
+
+
+
＜2．
∴
| a |
| a+b+d |
| b |
| b+c+a |
| c |
| c+d+b |
| d |
| d+a+c |
| a |
| a+b+c+d |
| b |
| a+b+c+d |
| c |
| a+b+c+d |
| d |
| a+b+c+d |
| a |
| a+b+d |
| b |
| b+c+a |
| c |
| c+d+b |
| d |
| d+a+c |
| a+c |
| a+b+c+d |
| b+d |
| a+b+c+d |
| c+a |
| a+b+c+d |
| d+b |
| a+b+c+d |
综上可得，1＜
| a |
| a+b+d |
| b |
| b+c+a |
| c |
| c+d+b |
| d |
| d+a+c |
点评：本题主要考查用放缩法证明不等式，不等式性质的应用，掌握好放缩的程度，是解此类题的难点，属于中档题．
练习册系列答案
相关题目
．
．
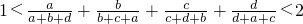