题目内容
设函数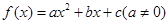 ,曲线
,曲线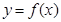 通过点(0,2a+3),且在
通过点(0,2a+3),且在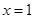 处的切线垂直于y轴.
处的切线垂直于y轴.
(I)用a分别表示b和c;
(II)当bc取得最大值时,写出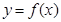 的解析式;
的解析式;
(III)在(II)的条件下,若函数 g(x)为偶函数,且当
g(x)为偶函数,且当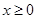 时,
时,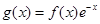 ,求当
,求当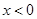 时g(x)的表达式,并求函数g(x)在R上的最小值及相应的x值.
时g(x)的表达式,并求函数g(x)在R上的最小值及相应的x值.
【答案】
(I)由已知可得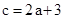 ,
,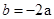 .
.
(II)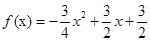 .
.
(III)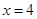 时,
时,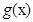 的最大值是
的最大值是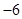 .
.
【解析】
试题分析:(I)根据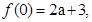 及导数的几何意义
及导数的几何意义 即得到
即得到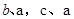 的关系.
的关系.
(II)将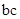 表示成
表示成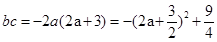 ,应用二次函数知识,当
,应用二次函数知识,当 时,
时, 取到最大值,得到
取到最大值,得到 ,从而得到
,从而得到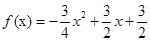 .
.
(III)首先由函数
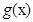 为偶函数,且当
为偶函数,且当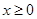 时,
时,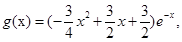
得到当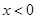 时,
时, 通过求导数并讨论时
通过求导数并讨论时
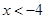 时,
时,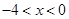 时,
时,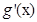 的正负号,明确
的正负号,明确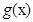 在区间
在区间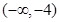 是减函数,在
是减函数,在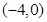 是增函数,
是增函数,
肯定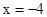 时,
时,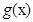 有最小值
有最小值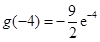 .
.
再根据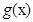 为偶函数,得到
为偶函数,得到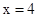 时,
时,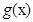 也有最小值
也有最小值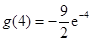 ,
,
作出结论.
试题解析:(I)由已知可得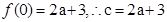
又因为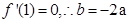 .
.
(II)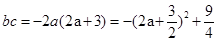 ,
,
所以当 时,
时, 取到最大值,此时
取到最大值,此时 ,
,
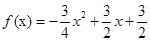 .
.
(III)因为,函数
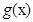 为偶函数,且当
为偶函数,且当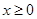 时,
时,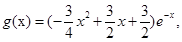
所以,当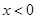 时,
时,
此时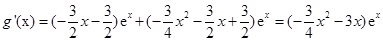 ,
,
当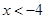 时,
时,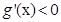 ,当
,当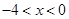 时,
时,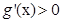 ,
,
所以,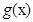 在区间
在区间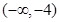 是减函数,在
是减函数,在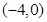 是增函数,
是增函数,
所以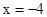 时,
时,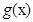 有最小值
有最小值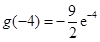 .
.
又因为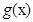 为偶函数,故当
为偶函数,故当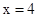 时,
时,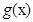 也有最小值
也有最小值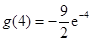 ,
,
综上可知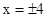 时,
时,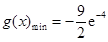 .
.
考点:二次函数的性质,导数的几何意义,应用导数研究函数的单调性、极值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,曲线
,曲线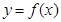 通过点(0,2a+3),且在
通过点(0,2a+3),且在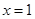 处的切线垂直于y轴.
处的切线垂直于y轴.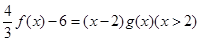 ,求g(x)的最大值及相应x值.
,求g(x)的最大值及相应x值.