题目内容
已知函数![]() .
.
(Ⅰ)若曲线C:y=f(x)在点P(0,1)处的切线l与曲线C有且只有一个公共点,求m的值;
(Ⅱ)求证:函数f(x)存在单调递减区间[a,b],并求出单调递减区间的长度t=b-a的取值范围.
答案:
解析:
解析:
|
解:(Ⅰ)函数 所以曲线 因为切线与曲线有唯一的公共点, 所以方程 令 ①当 所以 ②当 在区间 所以函数 而当 即当 综上讨论得 (Ⅱ) 因为 所以方程 即 所以函数 由于 所以函数 |

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
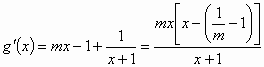
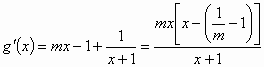 得
得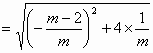

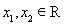
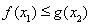
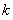
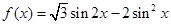 .
.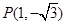 在角
在角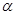 的终边上,求
的终边上,求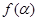 的值;(Ⅱ)若
的值;(Ⅱ)若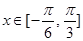 ,求
,求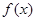 的值域.
的值域.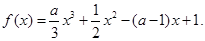
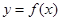 在点
在点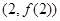 处的切线与直线
处的切线与直线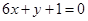 平行,求出这条切线的方程;
平行,求出这条切线的方程;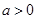 ,讨论函数
,讨论函数 的单调区间;
的单调区间;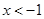 ,恒有
,恒有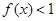 ,求实数
,求实数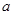 的取值范围.
的取值范围.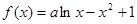 .
.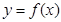 在
在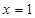 处的切线方程为
处的切线方程为 ,求实数
,求实数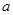 和
和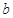 的值;
的值;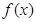 的单调性;
的单调性; 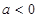 ,且对任意
,且对任意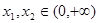 ,都有
,都有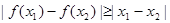 ,求
,求