题目内容
已知 ,a∈R.
,a∈R.(1)求f(x)的解析式;
(2)求f(x)的值域;
(3)设h(x)=2-xf(x),a>0时,对任意x1,x2∈[-1,1]总有
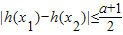 成立,求a的取值范围.
成立,求a的取值范围.
【答案】分析:(1)令t=log2x,则x=2t,故f(t)=a(2t)2-2•2t+1-a.从而得出f(x)的解析式;
(2)设m=2x,则m>0,y=am2-2m+1-a,下面对a进行分类讨论:①当a=0时,②当a>0时,③当a<0时,分别求出其值域即可;
(3)函数h(x)=a•2x+(1-a)2-x-2对任意x1,x2∈[-1,1],|h(x1)-h(x2)|≤ 恒成立,等价于h(x)在[-1,1]内满足其最大值与最小值的差小于等于
恒成立,等价于h(x)在[-1,1]内满足其最大值与最小值的差小于等于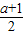 .
.
解答:解:(1)令t=log2x,则x=2t,
故f(t)=a(2t)2-2•2t+1-a.
∴f(x)=a(2x)2-2•2x+1-a,
(2)再设m=2x,则m>0,y=am2-2m+1-a,
①当a=0时,y=-2m+1(m>0),在(0,+∞)上是减函数,其值域为(-∞,1);
②当a>0时,y=am2-2m+1-a的对称轴m= >0,
>0,
故其在(0, )上是减函数,在(
)上是减函数,在(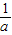 ,+∞)上是增函数.其值域为(-
,+∞)上是增函数.其值域为(- +1-a,+∞);
+1-a,+∞);
③当a<0时,y=am2-2m+1-a的对称轴m= <0,
<0,
故其在(0,+∞)上是减函数.其值域为(-∞,1-a);
(3)∵h(x)=a•2x+(1-a)2-x-2,
∴h′(x)=aln2•2x-(1-a)lna•2-x,
由h′(x)=aln2•2x-(1-a)lna•2-x=0,得x= log2
log2 (0<a<1).
(0<a<1).
由x= log2
log2 >1得0<a<
>1得0<a< ,由x=
,由x= log2
log2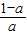 <-1,得a>
<-1,得a> ,
,
∵h(0)=-1,h(1)= (a-1),
(a-1),
由f(1)>f(0),得 (a-1)>-1,得a>
(a-1)>-1,得a> .
.
①当0<a≤ 时,h′(x)=aln2•2x-(1-a)lna•2-x<0恒成立,函数h(x)在[-1,1]上是减函数,
时,h′(x)=aln2•2x-(1-a)lna•2-x<0恒成立,函数h(x)在[-1,1]上是减函数,
∴函数h(x)在[-1,1]内的最大值是h(-1)=- a,最小值是h(1)=
a,最小值是h(1)= (a-1).
(a-1).
∵对任意x1,x2∈[-1,1]总有 成立,
成立,
∴- a-
a- (a-1)≤
(a-1)≤ ,∴a≥2.不合,舍去.
,∴a≥2.不合,舍去.
②当 <a≤
<a≤ 时,函数h(x)在[-1,x]上是减函数,在(x,1]上是增函数
时,函数h(x)在[-1,x]上是减函数,在(x,1]上是增函数
∴函数h(x)在[-1,1]内的最大值是h(-1)=- a,最小值是h(x)=2
a,最小值是h(x)=2 -2.
-2.
∵对任意x1,x2∈[-1,1]总有 成立,
成立,
∴- a-2
a-2 +2≤
+2≤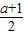 ,
,
∴ ≥a≥
≥a≥ .
.
③当 <a≤
<a≤ 时,函数h(x)在[-1,x]上是减函数,在(x,1]上是增函数
时,函数h(x)在[-1,x]上是减函数,在(x,1]上是增函数
∴函数h(x)在[-1,1]内的最大值是h(1)= (a-1),最小值是h(x)=2
(a-1),最小值是h(x)=2 -2.
-2.
∵对任意x1,x2∈[-1,1]总有 成立,
成立,
∴ (a-1)-2
(a-1)-2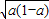 +2≤
+2≤ ,
,
∴ <a≤
<a≤ .
.
④当a> 时,h′(x)=aln2•2x-(1-a)lna•2-x>0恒成立,函数h(x)在[-1,1]上是增函数,
时,h′(x)=aln2•2x-(1-a)lna•2-x>0恒成立,函数h(x)在[-1,1]上是增函数,
∴函数h(x)在[-1,1]内的最大值是h(1),最小值是h(-1).
∵对任意x1,x2∈[-1,1]总有 成立,
成立,
∴ (a-1)+
(a-1)+ a≤
a≤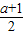 ,
,
∴a≤ .不合,舍去.
.不合,舍去.
综上所述,a的取值范围为[ ,
, ].
].
点评:本题考查函数的值域,考查满足条件的实数的取值范围的求法,考查分类讨论的思想.解题的关键是要分析出|f(x1)-f(x2)|≤f(x)max-f(x)min.
(2)设m=2x,则m>0,y=am2-2m+1-a,下面对a进行分类讨论:①当a=0时,②当a>0时,③当a<0时,分别求出其值域即可;
(3)函数h(x)=a•2x+(1-a)2-x-2对任意x1,x2∈[-1,1],|h(x1)-h(x2)|≤
 恒成立,等价于h(x)在[-1,1]内满足其最大值与最小值的差小于等于
恒成立,等价于h(x)在[-1,1]内满足其最大值与最小值的差小于等于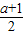 .
.解答:解:(1)令t=log2x,则x=2t,
故f(t)=a(2t)2-2•2t+1-a.
∴f(x)=a(2x)2-2•2x+1-a,
(2)再设m=2x,则m>0,y=am2-2m+1-a,
①当a=0时,y=-2m+1(m>0),在(0,+∞)上是减函数,其值域为(-∞,1);
②当a>0时,y=am2-2m+1-a的对称轴m=
 >0,
>0,故其在(0,
 )上是减函数,在(
)上是减函数,在(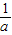 ,+∞)上是增函数.其值域为(-
,+∞)上是增函数.其值域为(- +1-a,+∞);
+1-a,+∞);③当a<0时,y=am2-2m+1-a的对称轴m=
 <0,
<0,故其在(0,+∞)上是减函数.其值域为(-∞,1-a);
(3)∵h(x)=a•2x+(1-a)2-x-2,
∴h′(x)=aln2•2x-(1-a)lna•2-x,
由h′(x)=aln2•2x-(1-a)lna•2-x=0,得x=
 log2
log2 (0<a<1).
(0<a<1).由x=
 log2
log2 >1得0<a<
>1得0<a< ,由x=
,由x= log2
log2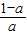 <-1,得a>
<-1,得a> ,
,∵h(0)=-1,h(1)=
 (a-1),
(a-1),由f(1)>f(0),得
 (a-1)>-1,得a>
(a-1)>-1,得a> .
.①当0<a≤
 时,h′(x)=aln2•2x-(1-a)lna•2-x<0恒成立,函数h(x)在[-1,1]上是减函数,
时,h′(x)=aln2•2x-(1-a)lna•2-x<0恒成立,函数h(x)在[-1,1]上是减函数,∴函数h(x)在[-1,1]内的最大值是h(-1)=-
 a,最小值是h(1)=
a,最小值是h(1)= (a-1).
(a-1).∵对任意x1,x2∈[-1,1]总有
 成立,
成立,∴-
 a-
a- (a-1)≤
(a-1)≤ ,∴a≥2.不合,舍去.
,∴a≥2.不合,舍去.②当
 <a≤
<a≤ 时,函数h(x)在[-1,x]上是减函数,在(x,1]上是增函数
时,函数h(x)在[-1,x]上是减函数,在(x,1]上是增函数∴函数h(x)在[-1,1]内的最大值是h(-1)=-
 a,最小值是h(x)=2
a,最小值是h(x)=2 -2.
-2.∵对任意x1,x2∈[-1,1]总有
 成立,
成立,∴-
 a-2
a-2 +2≤
+2≤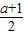 ,
,∴
 ≥a≥
≥a≥ .
.③当
 <a≤
<a≤ 时,函数h(x)在[-1,x]上是减函数,在(x,1]上是增函数
时,函数h(x)在[-1,x]上是减函数,在(x,1]上是增函数∴函数h(x)在[-1,1]内的最大值是h(1)=
 (a-1),最小值是h(x)=2
(a-1),最小值是h(x)=2 -2.
-2.∵对任意x1,x2∈[-1,1]总有
 成立,
成立,∴
 (a-1)-2
(a-1)-2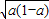 +2≤
+2≤ ,
,∴
 <a≤
<a≤ .
.④当a>
 时,h′(x)=aln2•2x-(1-a)lna•2-x>0恒成立,函数h(x)在[-1,1]上是增函数,
时,h′(x)=aln2•2x-(1-a)lna•2-x>0恒成立,函数h(x)在[-1,1]上是增函数,∴函数h(x)在[-1,1]内的最大值是h(1),最小值是h(-1).
∵对任意x1,x2∈[-1,1]总有
 成立,
成立,∴
 (a-1)+
(a-1)+ a≤
a≤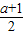 ,
,∴a≤
 .不合,舍去.
.不合,舍去.综上所述,a的取值范围为[
 ,
, ].
].点评:本题考查函数的值域,考查满足条件的实数的取值范围的求法,考查分类讨论的思想.解题的关键是要分析出|f(x1)-f(x2)|≤f(x)max-f(x)min.

练习册系列答案
相关题目
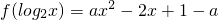 ,a∈R.
,a∈R.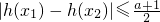 成立,求a的取值范围.
成立,求a的取值范围. ,a∈R.
,a∈R.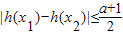 成立,求a的取值范围.
成立,求a的取值范围.