题目内容
【题目】如图所示,EP交圆于E,C两点,PD切圆于D,G为CE上一点且PG=PD,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F. 
(1)求证:BD⊥AD;
(2)若AC=BD,AB=6,求弦DE的长.
【答案】
(1)证明:∵PG=PD,∴∠PDG=∠PGD,
由于PD为切线,故∠PDA=∠DBA,
又∵∠EGA=∠PGD,∴∠EGA=∠DBA,
∴∠DBA+∠BAD=∠EGA+∠BAD,
从而∠PFA=∠BDA.
又AF⊥EP,∴∠PFA=90°,则∠BDA=90°,
故AB为圆的直径,
∴BD⊥AD.
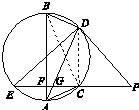
(2)解:连接BC,DC.
由于AB是直径,故∠BDA=∠ACB=90°.
在Rt△BDA与Rt△ACB中,AB=BA,AC=BD,从而得Rt△BDA≌Rt△ACB,
于是∠DAB=∠CBA.
又∵∠DCB=∠DAB,∴∠DCB=∠CBA,故DC∥AB.
∵AB⊥EP,∴DC⊥EP,∠DCE为直角,
∴ED为直径,又由(1)知AB为圆的直径,
∴DE=AB=6
【解析】(1)由已知PG=PD,得到∠PDG=∠PGD,由切割弦定理得到∠PDA=∠DBA,进一步得到∠EGA=∠DBA,从而∠PFA=∠BDA.最后可得∠BDA=90°,说明AB为圆的直径;(2)连接BC,DC.由AB是直径得到∠BDA=∠ACB=90°,然后由Rt△BDA≌Rt△ACB,得到∠DAB=∠CBA.再由∠DCB=∠DAB可推得DC∥AB.进一步得到ED为直径,则ED长可求.

 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案【题目】2016年04月13日“山东济南非法经营疫苗系列案件”披露后,引发社会高度关注,引起公众、受种者和儿童家长对涉案疫苗安全性和有效性的担忧。为采取后续处置措施提供依据,保障受种者的健康,尽快恢复公众接种疫苗的信心,科学严谨地分析涉案疫苗接种给受种者带来的安全性风险和是否有效,对某疫苗预防疾病的效果,进行动物实验,得到下面表格中的统计数据:现从所有试验动物中任取一只,取到“注射疫苗”动物的概率为![]() .
.
未发病 | 发病 | 合计 | |
未注射疫苗 |
|
|
|
注射疫苗 |
|
|
|
合计 |
|
|
|
(1)求![]() 列联表中的数据
列联表中的数据![]() 的值;
的值;
(2)绘制发病率的条形统计图,并判断疫苗是否有效?

|
|
|
|
|
|
|
|
|
|
(3)能够有多大把握认为疫苗有效?
附:![]()
【题目】某销售公司拟招聘一名产品推销员,有如下两种工资方案:
方案一:每月底薪2000元,每销售一件产品提成15元;
方案二:每月底薪3500元,月销售量不超过300件,没有提成,超过300件的部分每件提成30元.
(1)分别写出两种方案中推销员的月工资![]() (单位:元)与月销售产品件数
(单位:元)与月销售产品件数![]() 的函数关系式;
的函数关系式;
(2)从该销售公司随机选取一名推销员,对他(或她)过去两年的销售情况进行统计,得到如下统计表:
月销售产品件数 | 300 | 400 | 500 | 600 | 700 |
次数 | 2 | 4 | 9 | 5 | 4 |
把频率视为概率,分别求两种方案推销员的月工资超过11090元的概率.