题目内容
一个口袋中有4个白球,2个黑球,每次从袋中取出一个球.
(1)若有放回的取2次球,求第二次取出的是黑球的概率;
(2)若不放回的取2次球,求在第一次取出白球的条件下,第二次取出的是黑球的概率;
(3)若有放回的取3次球,求取出黑球次数X的分布列及E(X).
(1)若有放回的取2次球,求第二次取出的是黑球的概率;
(2)若不放回的取2次球,求在第一次取出白球的条件下,第二次取出的是黑球的概率;
(3)若有放回的取3次球,求取出黑球次数X的分布列及E(X).
设Ai=“第i次取到白球”,Bi=“第i次取到黑球”
(1)每次均从6个球中取球,每次取球的结果互不影响,
所以P(B2)=
.…(3分)
(2)问题相当于“从3个白球,2个黑球中取一次球,求取到黑球的概率”,
所以,所求概率P=
.…(6分)
(3)有放回的依次取出3个球,则取到黑球次数X的可能取值为0,1,2,3.…(7分)
三次取球互不影响,由(1)知每次取出黑球的概率均为
,
所以,P(X=0)=
(
)3=
;
P(X=1)=
(
)•(
)2=
;
P(X=2)=
(
)2•(
)1=
;
P(X=3)=
(
)3=
.…(9分)
…(10分)
这个试验为3次独立重复事件,X服从二项分布,即X\~B(3,
),所以,E(X)=1.…(12分)
(1)每次均从6个球中取球,每次取球的结果互不影响,
所以P(B2)=
| 1 |
| 3 |
(2)问题相当于“从3个白球,2个黑球中取一次球,求取到黑球的概率”,
所以,所求概率P=
| 2 |
| 5 |
(3)有放回的依次取出3个球,则取到黑球次数X的可能取值为0,1,2,3.…(7分)
三次取球互不影响,由(1)知每次取出黑球的概率均为
| 1 |
| 3 |
所以,P(X=0)=
| C | 03 |
| 2 |
| 3 |
| 8 |
| 27 |
P(X=1)=
| C | 13 |
| 1 |
| 3 |
| 2 |
| 3 |
| 4 |
| 9 |
P(X=2)=
| C | 23 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
P(X=3)=
| C | 33 |
| 1 |
| 3 |
| 1 |
| 27 |
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
这个试验为3次独立重复事件,X服从二项分布,即X\~B(3,
| 1 |
| 3 |

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
 ,
, ,
, ,
, (
( ,第二次出现底面朝下的复数记为
,第二次出现底面朝下的复数记为 .
. 表示“
表示“ ”这一事件,求事件
”这一事件,求事件 ;
; 的实部为
的实部为 ,求
,求 .有放回地摸球,每次摸出一个,有3次摸到红球即停止.
.有放回地摸球,每次摸出一个,有3次摸到红球即停止. 为合格品的概率为
为合格品的概率为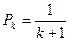 (
( 1,2,3),设各次制造的零件合格与否是相互独立的,以
1,2,3),设各次制造的零件合格与否是相互独立的,以 表示合格品的个数,求
表示合格品的个数,求
 ,且各件产品是否为优质品相互独立.
,且各件产品是否为优质品相互独立.