题目内容
某汽车生产企业,上年度生产汽车的投入成本为8万元/辆,出厂价为10万元/辆,年销售量为12万辆.本年度为节能减排,对产品进行升级换代.若每辆车投入成本增加的比例为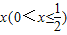 ,则出厂价相应提高的比例为0.75x,同时预计年销售量增加的比例为0.5x.
,则出厂价相应提高的比例为0.75x,同时预计年销售量增加的比例为0.5x.(1)写出本年度预计的年利润y与投入成本增加的比例x的关系式;
(2)当投入成本增加的比例x为何值时,本年度比上年度利润增加最多?最多为多少?
【答案】分析:(1)由题意可知,本年度每辆车的利润为10(1+0.75x)-8(1+x),本年度的销售量是12(1+0.5x),由此能求出年利润y与投入成本增加的比例x的关系式.
(2)设本年度比上年度利润增加为f(x),则f(x)=(-3x2+6x+24)-24=-3(x-1)2+3,因为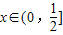 ,在区间
,在区间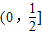 上f(x)为增函数,由此能求出当投入成本增加的比例x为何值时,本年度比上年度利润增加最多,交能求出最多为多少.
上f(x)为增函数,由此能求出当投入成本增加的比例x为何值时,本年度比上年度利润增加最多,交能求出最多为多少.
解答:解:(1)由题意可知,本年度每辆车的利润为10(1+0.75x)-8(1+x)
本年度的销售量是12(1+0.5x),
故年利润y=12(1+0.5x)[10(1+0.75x)-8(1+x)]
=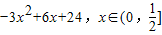 .…(6分)
.…(6分)
(2)设本年度比上年度利润增加为f(x),
则f(x)=(-3x2+6x+24)-24=-3(x-1)2+3,
因为 ,
,
在区间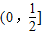 上f(x)为增函数,
上f(x)为增函数,
所以当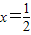 时,函数y=f(x)有最大值为
时,函数y=f(x)有最大值为 .
.
故当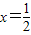 时,本年度比上年度利润增加最多,
时,本年度比上年度利润增加最多,
最多为2.25亿元.…(16分)
点评:本题考查函数模型的选择与应用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答.
(2)设本年度比上年度利润增加为f(x),则f(x)=(-3x2+6x+24)-24=-3(x-1)2+3,因为
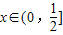 ,在区间
,在区间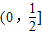 上f(x)为增函数,由此能求出当投入成本增加的比例x为何值时,本年度比上年度利润增加最多,交能求出最多为多少.
上f(x)为增函数,由此能求出当投入成本增加的比例x为何值时,本年度比上年度利润增加最多,交能求出最多为多少.解答:解:(1)由题意可知,本年度每辆车的利润为10(1+0.75x)-8(1+x)
本年度的销售量是12(1+0.5x),
故年利润y=12(1+0.5x)[10(1+0.75x)-8(1+x)]
=
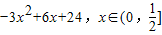 .…(6分)
.…(6分)(2)设本年度比上年度利润增加为f(x),
则f(x)=(-3x2+6x+24)-24=-3(x-1)2+3,
因为
 ,
,在区间
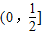 上f(x)为增函数,
上f(x)为增函数,所以当
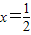 时,函数y=f(x)有最大值为
时,函数y=f(x)有最大值为 .
.故当
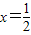 时,本年度比上年度利润增加最多,
时,本年度比上年度利润增加最多,最多为2.25亿元.…(16分)
点评:本题考查函数模型的选择与应用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
相关题目