题目内容
 (2013•鹰潭一模)一个空间几何体的三视图如图所示,则该几何体外接球的表面积为
(2013•鹰潭一模)一个空间几何体的三视图如图所示,则该几何体外接球的表面积为64π
64π
.分析:根据三视图的定义与性质,可得该几何体是底面边长为6,且高等于4的正三棱柱.因此,外接球球心在上、下底面中心连线段的中点.根据正三角形的性质,算出AH=
AB=2
,Rt△AHO中利用勾股定理算出AO=4,得外接球半径R=4,再用球的表面积公式,即可求出该几何体外接球的表面积.
| ||
| 3 |
| 3 |
解答:解:根据题意,得该几何体是底面边长为6,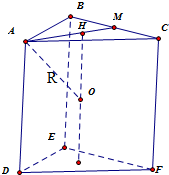 且高等于4的正三棱柱
且高等于4的正三棱柱
设正三棱柱为如图的三棱柱ABC-DEF,
可得该几何体外接球的外接球球心为上、下底面中心的连线段的中点
设外接球球心为0点,上底面中心为H,(H为△ABC中线AM的三等分点)
∵正△ABC边长为6,
∴AM=
AB=3
,可得AH=
AM=2
Rt△AHO中,HO=
AD=2,
∴AO=
=4,即外接球半径R=4
因此,该几何体外接球的表面积为S=4πR2=64π
故答案为:64π
 且高等于4的正三棱柱
且高等于4的正三棱柱设正三棱柱为如图的三棱柱ABC-DEF,
可得该几何体外接球的外接球球心为上、下底面中心的连线段的中点
设外接球球心为0点,上底面中心为H,(H为△ABC中线AM的三等分点)
∵正△ABC边长为6,
∴AM=
| ||
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
Rt△AHO中,HO=
| 1 |
| 2 |
∴AO=
| AH2+HO2 |
因此,该几何体外接球的表面积为S=4πR2=64π
故答案为:64π
点评:本题将一个多面体的三视图还原,并求它的外接球的表面积,着重考查了三视图的定义与性质、正三棱柱的外接球等知识,属于中档题.

练习册系列答案
相关题目