题目内容
（2013•鹰潭一模）定义域为R的偶函数f（x）满足对?x∈R，有f（x+2）=f（x）-f（1），且当x∈[2，3]时，f（x）=-2x2+12x-18，若函数y=f（x）-loga（|x|+1）在（0，+∞）上至多三个零点，则a的取值范围是（ ）
分析：先利用函数是偶函数求出，f（1），进而得到函数的周期性，然后利用函数的周期性和奇偶性作出函数f（x）的图象，利用f（x）与loga（|x|+1）的图象关系确定取值范围．
解答：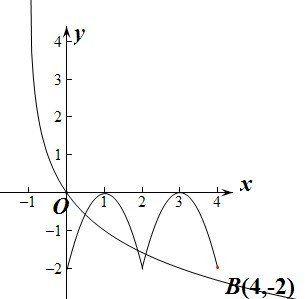
解：因为函数f（x）是偶函数，所以令x=-1得，f（-1+2）=f（-1）-f（1）=f（1），解得f（1）=0，所以f（x+2）=f（x）-f（1）=f（x），即函数的周期是2．
由y=f（x）-loga（|x|+1）=0得f（x）=loga（|x|+1），令y=f（x），y=loga（|x|+1），当x＞0时，y=loga（|x|+1）=loga（x+1），函数过点（0，0）．
若a＞1，则由图象可知，此时数y=f（x）-loga（|x|+1）在（0，+∞）上没有零点，所以此时此时满足条件．
若0＜a＜1，则由图象可知，要使两个函数y=f（x）与y=loga（x+1），有三个交点，
则y=m（x）=loga（x+1）不能过点B（4，-2），即m（4）＜-2，即loga5＜-2，解得a＞
，此时
＜a＜1．
所以满足条件的a的取值范围a＞1或
＜a＜1．
故选B．
解：因为函数f（x）是偶函数，所以令x=-1得，f（-1+2）=f（-1）-f（1）=f（1），解得f（1）=0，所以f（x+2）=f（x）-f（1）=f（x），即函数的周期是2．由y=f（x）-loga（|x|+1）=0得f（x）=loga（|x|+1），令y=f（x），y=loga（|x|+1），当x＞0时，y=loga（|x|+1）=loga（x+1），函数过点（0，0）．
若a＞1，则由图象可知，此时数y=f（x）-loga（|x|+1）在（0，+∞）上没有零点，所以此时此时满足条件．
若0＜a＜1，则由图象可知，要使两个函数y=f（x）与y=loga（x+1），有三个交点，
则y=m（x）=loga（x+1）不能过点B（4，-2），即m（4）＜-2，即loga5＜-2，解得a＞
| ||
| 5 |
| ||
| 5 |
所以满足条件的a的取值范围a＞1或
| ||
| 5 |
故选B．
点评：本题考查了函数与方程以及函数零点个数问题，解决此类问题的基本方法是利用数形结合，将函数零点问题转化为两个函数图象的交点个数问题．
练习册系列答案
相关题目