题目内容
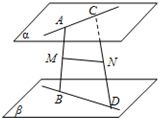 设平面α∥β,两条异面直线AC和BD分别在平面α、β内,线段AB、CD中点分别为M、N,设MN=a,线段AC=BD=2a,求异面直线AC和BD所成的角.
设平面α∥β,两条异面直线AC和BD分别在平面α、β内,线段AB、CD中点分别为M、N,设MN=a,线段AC=BD=2a,求异面直线AC和BD所成的角.
分析:取AD的中点为P,则PM、PN分别为三角形ADB、三角形DAC的中位线,,∠MPN即为异面直线AC和BD所成的角.
根据三边长,可得△PMN为等边三角形,∠MPN=60°,即得答案.
根据三边长,可得△PMN为等边三角形,∠MPN=60°,即得答案.
解答:解:连接AD,取AD的中点为P,连接PM 和PN,则PM、PN分别为三角形ADB、三角形DAC的中位线,
∴PM∥BD,PN∥AC,∠MPN即为异面直线AC和BD所成的角.
∵PM=
BD=a,PN=
AC=a,MN=a,∴△PMN为等边三角形,∴∠MPN=60°,
即异面直线AC和BD所成的角为 60°.
∴PM∥BD,PN∥AC,∠MPN即为异面直线AC和BD所成的角.
∵PM=
| 1 |
| 2 |
| 1 |
| 2 |
即异面直线AC和BD所成的角为 60°.
点评:本题考查异面直线所成的角的定义和求法,找出,∠MPN即为异面直线AC和BD所成的角,是解题的关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 在平面直角坐标系xOy中,已知⊙C1:(x+3)2+(y-1)2=4和⊙C2:(x-5)2+(y-1)2=4
在平面直角坐标系xOy中,已知⊙C1:(x+3)2+(y-1)2=4和⊙C2:(x-5)2+(y-1)2=4